题目内容
7.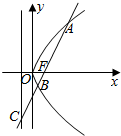 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 作AM、BN垂直准线于点M、N,根据$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,和抛物线的定义,可得tan∠NCB=2,从而可得直线方程,与抛物线方程联立,利用抛物线的定义,即可得出结论.
解答 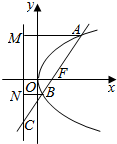 解:设A(x1,y1),B(x2,y2),
解:设A(x1,y1),B(x2,y2),
作AM、BN垂直准线于点M、N,则|BN|=|BF|,
∵$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,∴sin∠NCB=$\frac{\sqrt{5}}{5}$,
∴tan∠NCB=2
∴AF的方程为y=2(x-1),
代入y2=4x,可得x2-3x+1=0
∴x1+x2=3,
∴|AB|=x1+x2+2=5.
故选:B.
点评 此题是个中档题.考查抛物线的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
17.等比数列{an}中,a5、a7是函数f(x)=x2-4x+3的两个零点,则a3•a9等于( )
| A. | -4 | B. | -3 | C. | 4 | D. | 3 |
15.如图是一个几何体的三视图,则该几何体的体积为( )


| A. | $\frac{80}{3}$ | B. | $\frac{70}{3}$ | C. | 23 | D. | 24 |
16.在平面直角坐标系xOy中,若曲线y=2x2+$\frac{a}{x}$(a是常数)过点P(-1,-30),则函数y=2x2+$\frac{a}{x}$在区间[1,4]的最大值与最小值的和为64.
17.已知菱形ABCD的边长为为4,∠ABC=$\frac{π}{3}$,向其内部随机投放一点P,则点P与菱形各顶点距离均大于1的概率为( )
| A. | 1-$\frac{\sqrt{3}π}{24}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{24}$ | D. | $\frac{\sqrt{3}π}{12}$ |