题目内容
16.在平面直角坐标系xOy中,若曲线y=2x2+$\frac{a}{x}$(a是常数)过点P(-1,-30),则函数y=2x2+$\frac{a}{x}$在区间[1,4]的最大值与最小值的和为64.分析 由题意可得2-a=-30,解得a,再求函数的导数和单调区间、极值可得最小值,再计算端点的函数值,可得最大值,进而得到所求和.
解答 解:由题意可得2-a=-30,
解得a=32,
则y=2x2+$\frac{32}{x}$导数为y′=4x-$\frac{32}{{x}^{2}}$,
由2<x<4,可得y′>0,函数递增,
1<x<2时,可得y′<0,函数递减.
即有x=2处取得极小值,也为最小值24,
x=1时,y=34;x=4时,y=40.
即有函数的最大值为40,
则最值之和为64.
故答案为:64.
点评 本题考查函数的最值的求法,注意运用导数,求得单调区间、极值和最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,若输出的p是720,则输入的N的值是( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
7.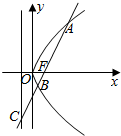 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.函数y=(x2-1)e|x|的图象大致是( )
| A. | 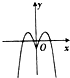 | B. | 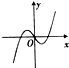 | C. | 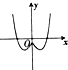 | D. | 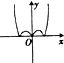 |
11.一个人将编号为1,2,3,4的四个小球随机放入编号为1,2,3,4的四个盒子中,每个盒子放一个小球,球的编号与盒子的编号相同时叫做放对了,否则叫做错了,设放对的个数为ξ,则ξ的期望值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
8.生产一批零件,其质量按测试指标划分为:指标大于或等于8为优质品,小于8大于等于4为正品,小于4为次品,现随机抽取这种零件100件进行检测,检测结果统计如下:据以上述测试中各组的频率作为相应的概率.
(1)试估计这种零件的平均质量指标;
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.
| 测试指标 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.