题目内容
18.长、宽、高分別为2,1,2的长方体的每个顶点都在同一个球面上,则该球的表面积为9π.分析 先求长方体的对角线的长度,就是球的直径,然后求出它的表面积.
解答 解:长方体的体对角线的长是:$\sqrt{4+1+4}$=3
球的半径是:$\frac{3}{2}$
这个球的表面积:4π$•\frac{9}{4}$=9π
故答案为:9π
点评 本题考查球的内接体,球的表面积,考查空间想象能力,是基础题.

练习册系列答案
相关题目
6.执行如图所示的程序框图,若输出的p是720,则输入的N的值是( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
10.执行如图所示的程序框图,若输出的a等于341,则判断框内应填写( )
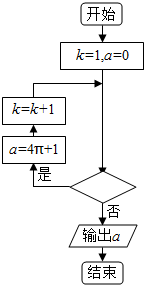

| A. | k<4? | B. | k<5? | C. | k<6? | D. | k<7? |
7.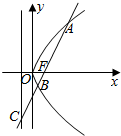 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.生产一批零件,其质量按测试指标划分为:指标大于或等于8为优质品,小于8大于等于4为正品,小于4为次品,现随机抽取这种零件100件进行检测,检测结果统计如下:据以上述测试中各组的频率作为相应的概率.
(1)试估计这种零件的平均质量指标;
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.
| 测试指标 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.
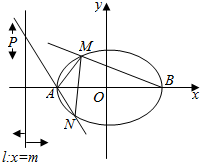 已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.
已知椭圆C的中心在原点,焦点在x轴上,离心率e=$\frac{\sqrt{3}}{2}$,短半轴长b=1.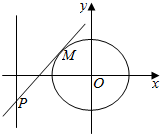 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.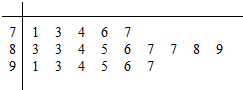 我市为了检测空气质量,每天都要记录空气质量指数(指数采用10分制,保留一位小数),现随机抽取20天的指数,绘制成如图所示的统计图(以整数部分为茎,小数部分为叶),设指数不低于8.5的视为当天空气质量为优良.
我市为了检测空气质量,每天都要记录空气质量指数(指数采用10分制,保留一位小数),现随机抽取20天的指数,绘制成如图所示的统计图(以整数部分为茎,小数部分为叶),设指数不低于8.5的视为当天空气质量为优良.