题目内容
12.过椭圆Г:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1外一点P(x0,y0)(x0≠±2且y0≠0)向椭圆Г作切线,切点分别为A、B,直线AB交y轴于M,记直线PA、PB、PM的斜率分别为k1、k2、k0.(1)当点P的坐标为(4,3)时,求直线AB的方程;
(2)当x0≠0时,是否存在常数λ,使得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{0}}$恒成立?若存在,求λ的值;若不存在,说明理由.
分析 (1)设切点A(x1,y1),B(x2,y2),M(0,m),对椭圆方程两边求导,可得切线的斜率,求得切线方程,再由两点确定一条直线,即可得到所求AB的方程;
(2)假设存在常数λ,使得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{0}}$恒成立.设过P的直线方程为y-y0=k(x-x0),代入椭圆方程,运用相切的条件,可得判别式为0,再由韦达定理可得k1、k2的关系式,再由AB的方程可得k0,再由恒成立思想,即可判断存在性.
解答 解:(1)设切点A(x1,y1),B(x2,y2),M(0,m),
由$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,两边对x求导,可得$\frac{1}{2}$x+$\frac{2}{3}$yy′=0,
即有PA的斜率为k1=-$\frac{3{x}_{1}}{4{y}_{1}}$,
直线PA的方程为y-y1=-$\frac{3{x}_{1}}{4{y}_{1}}$(x-x1),
又$\frac{{{x}_{1}}^{2}}{4}$+$\frac{{{y}_{1}}^{2}}{3}$=1,
即为$\frac{{x}_{1}x}{4}$+$\frac{{y}_{1}y}{3}$=1,
同理可得PB:$\frac{{x}_{2}x}{4}$+$\frac{{y}_{2}y}{3}$=1,
又点P的坐标为(4,3),可得
$\frac{4{x}_{1}}{4}$+$\frac{3{y}_{1}}{3}$=1,$\frac{4{x}_{2}}{4}$+$\frac{3{y}_{2}}{3}$=1,
由两点确定一条直线,可得
直线AB的方程为x+y=1;
(2)假设存在常数λ,使得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{0}}$恒成立.
设过P的直线方程为y-y0=k(x-x0),即为y=kx+y0-kx0,
代入椭圆方程3x2+4y2=12,
可得(3+4k2)x2+8k(y0-kx0)x+4(y0-kx0)2-12=0,
由直线和椭圆相切的条件,可得
判别式△=64k2(y0-kx0)2-16(3+4k2)[(y0-kx0)2-3]=0,
即为k2(x02-4)-2kx0y0+y02-3=0,
即有k1+k2=$\frac{2{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-4}$,k1k2=$\frac{{{y}_{0}}^{2}-3}{{{x}_{0}}^{2}-4}$,
由AB:$\frac{{x}_{0}x}{4}$+$\frac{{y}_{0}y}{3}$=1,可得M(0,$\frac{3}{{y}_{0}}$),
即有k0=$\frac{{{y}_{0}}^{2}-3}{{x}_{0}{y}_{0}}$,
由$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{0}}$,可得$\frac{{k}_{1}{+k}_{2}}{{k}_{1}{k}_{2}}$=$\frac{λ}{{k}_{0}}$,
即为$\frac{2{x}_{0}{y}_{0}}{{{y}_{0}}^{2}-3}$=$\frac{λ{x}_{0}{y}_{0}}{{{y}_{0}}^{2}-3}$,
即有λ=2.
则存在常数λ=2,使得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{0}}$恒成立.
点评 本题考查椭圆方程和运用,考查直线和椭圆相切的条件:判别式为0,考查直线的斜率公式的运用,属于中档题.

(1)根据以上数据建立一个2×2列联表,并判断在犯错误的概率不超过0.5%的前提下能否认为第一时间收看该类节目与性别有关?
(2)该研究性学习小组共有A、B、C、D和E五名同学,五人分成两组模拟“撕名牌”的游戏,其中一组三人,一组两人,求A、B两同学分在同一组的概率
参考数据:X2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
临界值表:
| P(X2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
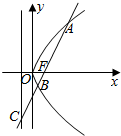 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$,则|AB|等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 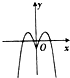 | B. | 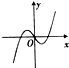 | C. | 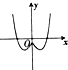 | D. | 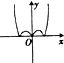 |
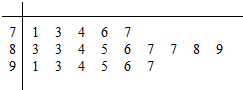 我市为了检测空气质量,每天都要记录空气质量指数(指数采用10分制,保留一位小数),现随机抽取20天的指数,绘制成如图所示的统计图(以整数部分为茎,小数部分为叶),设指数不低于8.5的视为当天空气质量为优良.
我市为了检测空气质量,每天都要记录空气质量指数(指数采用10分制,保留一位小数),现随机抽取20天的指数,绘制成如图所示的统计图(以整数部分为茎,小数部分为叶),设指数不低于8.5的视为当天空气质量为优良.