题目内容
17．已知菱形ABCD的边长为为4，∠ABC=$\frac{π}{3}$，向其内部随机投放一点P，则点P与菱形各顶点距离均大于1的概率为（ ）| A． | 1-$\frac{\sqrt{3}π}{24}$ | B． | 1-$\frac{\sqrt{3}π}{12}$ | C． | $\frac{\sqrt{3}π}{24}$ | D． | $\frac{\sqrt{3}π}{12}$ |
分析 根据几何概型的概率公式求出对应区域的面积进行求解即可．
解答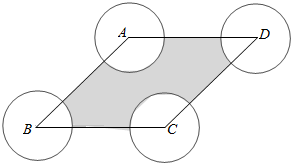 
解：分别以A，B，C，D为圆心，1为半径的圆，
则所以概率对应的面积为阴影部分，
则四个圆在菱形内的扇形夹角之和为2π，
则对应的四个扇形之和的面积为一个整圆的面积S=π×12=π，
∵S菱形ABCD=AB•BCsin$\frac{π}{3}$=4×4×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$，
∴S阴影=S菱形ABCD-S空白=8$\sqrt{3}$-π×12=8$\sqrt{3}$-π．
因此，该点到四个顶点的距离大于1的概率P=$\frac{{S}_{阴影}}{{S}_{菱形}}$=$1-\frac{{\sqrt{3}π}}{24}$，
故选：A．
点评 本题主要考查几何概型的概率的计算，根据对应分别求出对应区域的面积是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
7．
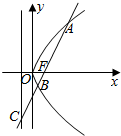如图，直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A，B，C，若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$，则|AB|等于（ ）
如图，直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A，B，C，若$\frac{|BF|}{|BC|}$=$\frac{\sqrt{5}}{5}$，则|AB|等于（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
8．生产一批零件，其质量按测试指标划分为：指标大于或等于8为优质品，小于8大于等于4为正品，小于4为次品，现随机抽取这种零件100件进行检测，检测结果统计如下：据以上述测试中各组的频率作为相应的概率．
（1）试估计这种零件的平均质量指标；
（2）生产一件零件，若是优质品可盈利40元，若是正品盈利20元，若是次品则亏损20元，若从大量的零件中随机抽取2件，其利润之和记为x（单位：元），求x的分布列及数学期望．
| 测试指标 | [0，2） | [2，4） | [4，6） | [6，8） | [8，10） |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
（2）生产一件零件，若是优质品可盈利40元，若是正品盈利20元，若是次品则亏损20元，若从大量的零件中随机抽取2件，其利润之和记为x（单位：元），求x的分布列及数学期望．