Question

已知双曲线C：

x2

a2

-

y2

b2

=1（a＞0，b＞0），F₁、F₂分别是它的左、右焦点，A（-1，0）是其左顶点，且双曲线的离心率为e=2．设过右焦点F₂的直线l与双曲线C的右支交于P、Q两点，其中点P位于第一象限内．
（1）求双曲线的方程；
（2）若直线AP、AQ分别与直线x=

1

2

交于M、N两点，求证：MF₂⊥NF₂；
（3）是否存在常数λ，使得∠PF₂A=λ∠PAF₂恒成立？若存在，求出λ的值，若不存在，请说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由题可知：a=1．由于e=

c

a

=2，可得c=2．再利用b²=c²-a²即可．
（2）设直线l的方程为：x=ty+2，另设：P（x₁，y₁）、Q（x₂，y₂）．联立

3x2-y2=3 x=ty+2

，可得根与系数的关系．又直线AP的方程为y=

y1

x1+1

(x+1)，解得M(

1

2

，

3y1

2(x1+1)

)．同理解得N(

1

2

，

3y2

2(x2+1)

)．只要证明

MF2

•

NF2

=0即可．
（3）当直线l的方程为x=2时，解得P（2，3）．易知此时△AF₂P为等腰直角三角形，可得：λ=2．
当∠AF₂P=2∠PAF₂对直线l存在斜率的情形也成立．利用正切的倍角公式、斜率计算公式、双曲线的方程、正切函数的单调性即可证明．

解答： （1）解：由题可知：a=1．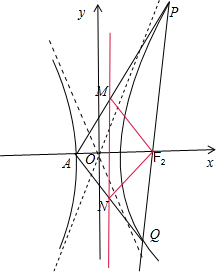
∵e=

c

a

=2，
∴c=2．
∴b²=c²-a²=3，
∴双曲线C的方程为：x2-

y2

3

=1．
（2）证明：设直线l的方程为：x=ty+2，另设：P（x₁，y₁），
Q（x₂，y₂）．
联立

3x2-y2=3 x=ty+2

，化为（3t²-1）y²+12ty+9=0．
∴y1+y2=

-12t

3t2-1

，y1y2=

9

3t2-1

．
又直线AP的方程为y=

y1

x1+1

(x+1)，代入x=

1

2

，
解得M(

1

2

，

3y1

2(x1+1)

)．
同理，直线AQ的方程为y=

y2

x2+1

(x+1)，代入x=

1

2

，解得N(

1

2

，

3y2

2(x2+1)

)．
∴

MF2

=(

3

2

，-

3y1

2(x1+1)

)，

NF2

=(

3

2

，

-3y2

2(x2+1)

)．
∴

MF2

•

NF2

=

9

4

+

9y1y2

4(x1+1)(x2+1)

=

9

4

+

9y1y2

4(ty1+1)(ty2+1)

=

9

4

+

9y1y2

4[t2y1y2+t(y1+y2)+1]

=

9

4

+

9× 9 3t2-1

4(t2× 9 3t2-1 +3t× -12t 3t2-1 +9)

=

9

4

-

9

4

=0．
∴MF₂⊥NF₂．
（3）解：当直线l的方程为x=2时，解得P（2，3）．易知此时△AF₂P为等腰直角三角形，
其中∠AF2P=

π

2

，∠PAF2=

π

4

，也即：λ=2．
下证：∠AF₂P=2∠PAF₂对直线l存在斜率的情形也成立．
tan2∠PAF₂=

2tan∠PAF2

1-tan2∠PAF2

=

2kPA

1- k 2 PA

=

2× y1 x1+1

1-( y1 x1+1 )2

=

2y1(x1+1)

(x1+1)2- y 2 1

．
∵

x

2 1

-

y 2 1

3

=1，∴

y

2 1

=3(

x

2 1

-1)．
∴tan2∠PAF2=

2y1(x1+1)

(x1+1)2-3(x1 2-1)

=

2y1(x1+1)

-2(x1+1)(x1-2)

=-

y1

x1-2

，
∴tan∠AF2P=-kPF2=-

y1

x1-2

=tan2∠PAF2，
∴结合正切函数在(0，

π

2

)∪(

π

2

，π)上的图象可知，∠AF₂P=2∠PAF₂．

点评：本题综合考查了双曲线的标准方程及其性质、向量垂直与数量积的关系、正切的倍角公式、斜率计算公式、双曲线的方程、正切函数的单调性等基础知识与基本技能方法，考查了推理能力与计算能力，属于难题．