题目内容
已知等差数列{an}满足:a3=7,a8+a4=26,{an}的前n项和为Sn.
(Ⅰ)求an及Sn;
(Ⅱ)令bn=
(n∈N*),求数列{bn}的前n项和Tn.
(Ⅰ)求an及Sn;
(Ⅱ)令bn=
| 1 |
| an2-1 |
考点:数列的求和,等差数列的前n项和
专题:等差数列与等比数列
分析:(Ⅰ)根据等差数列的通项公式求出首项和公差即可求an及Sn;
(Ⅱ)求出bn的通项公式,利用裂项法即可得到结论.
(Ⅱ)求出bn的通项公式,利用裂项法即可得到结论.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,因为a3=7,a8+a4=26,所以有
,解得a1=3,d=2,
所以an=3+2(n-1)=2n+1;Sn=3n+
×2=n2+2n.
(Ⅱ)由(Ⅰ)知an=2n+1,所以bn=
=
=
•
=
(
-
),
所以数列{bn}的前n项和Tn=
(1-
+
-
+…+
-
)=
(1-
)=
,
即数列{bn}的前n项和Tn=
.
|
所以an=3+2(n-1)=2n+1;Sn=3n+
| n(n-1) |
| 2 |
(Ⅱ)由(Ⅰ)知an=2n+1,所以bn=
| 1 |
| an2-1 |
| 1 |
| (2n+1)2-1 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
所以数列{bn}的前n项和Tn=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| n+1 |
| n |
| 4(n+1) |
即数列{bn}的前n项和Tn=
| n |
| 4(n+1) |
点评:本题主要考查等差数列的通项公式和前n项和的计算,以及利用裂项法进行求和.

练习册系列答案
相关题目
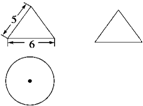 有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积及体积为( )
有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积及体积为( )| A、24π cm2,12π cm3 |
| B、15π cm2,12π cm3 |
| C、24π cm2,36π cm3 |
| D、以上都不正确 |
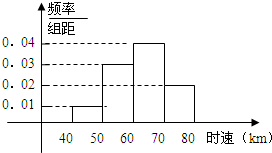 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示.
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示.