题目内容
f（x）=lnx+x2-3x的极大值点是（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
考点：利用导数研究函数的极值
专题：计算题,导数的综合应用
分析：求出函数的导数，令导数大于0，得增区间，令导数小于0，得减区间，注意定义域，由极值的定义，即可得到．
解答：
解：f（x）=lnx+x2-3x的导数f′（x）=
+2x-3（x＞0）=
，
令f′（x）＞0得x＞1或0＜x＜
，令f′（x）＜0得
＜x＜1．
则f（x）在x=
处导数左正右负，取得极大值，
故选A．
| 1 |
| x |
| (2x-1)(x-1) |
| x |
令f′（x）＞0得x＞1或0＜x＜
| 1 |
| 2 |
| 1 |
| 2 |
则f（x）在x=
| 1 |
| 2 |
故选A．
点评：本题考查了利用导数研究函数的极值，注意函数的定义域，属于基础题．
练习册系列答案
相关题目
在独立性检验中，统计量x2有两个临界值：3.841和6.635；当x2＞3.841时，有95%的把握说明两个事件有关，当x2＞6.635时，有99%的把握说明两个事件相关，当x2≤3.841时，认为两个事件无关．在一项调查某种药是否对心脏病有治疗作用时，共调查了3000人，经计算的x2=4.56，根据这一数据分析，认为此药物与心脏病之间（ ）
| A、有95%的把握认为两者相关 |
| B、约有95%的心脏病患者使用药物有作用 |
| C、有99%的把握认为两者相关 |
| D、约有99%的心脏病患者使用药物有作用 |
设
=（-2，1-cosθ），
=（1+cosθ，-
），且
∥
，则锐角θ=（ ）
| a |
| b |
| 1 |
| 4 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
阅读右侧程序框图，输出结果S的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
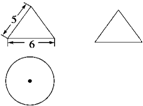有一个几何体的三视图及其尺寸如图所示（单位：cm），则该几何体的表面积及体积为（ ）| A、24π cm2，12π cm3 |
| B、15π cm2，12π cm3 |
| C、24π cm2，36π cm3 |
| D、以上都不正确 |
不等式|x-1|+|x+2|≤a的解集非空，则实数a的取值范围是（ ）
| A、a＞3 | B、a≥3 |
| C、a≤4 | D、a≥4 |
已知函数f（x）=sinx-lnx（0＜x＜2π）的零点为x0有0＜a＜b＜c＜2π使f（a）f（b）f（c）＞0则下列结论不可能成立的是（ ）
| A、x0＜a |
| B、x0＞b |
| C、x0＞c |
| D、x0＜π |