题目内容
已知
,
,
是三个向量,试判断下列各命题的真假.
(1)若
•
=
•
且
≠
,则
=
(2)向量
在
的方向上的投影是一模等于|
|cosθ(θ是
与
的夹角),方向与
在
相同或相反的一个向量.
| a |
| b |
| c |
(1)若
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
(2)向量
| a |
| b |
| a |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)由
•
=
•
且
≠
,可得
•(
-
)=0,可得
⊥(
-
),或
=
.
(2)由于向量
在
的方向上的投影是个数量,而非向量,即可判断出.
| a |
| b |
| a |
| c |
| a |
| 0 |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
(2)由于向量
| a |
| b |
解答:
解:(1)由
•
=
•
且
≠
,可得
•(
-
)=0,可得
⊥(
-
),或
=
.
因此这是一个假命题.
(2)向量
在
的方向上的投影是一模等于|
|cosθ(θ是
与
的夹角),方向与
在
相同或相反的一个向量.这是一个假命题.
因为向量
在
的方向上的投影是个数量,而非向量.
| a |
| b |
| a |
| c |
| a |
| 0 |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
因此这是一个假命题.
(2)向量
| a |
| b |
| a |
| a |
| b |
| a |
| b |
因为向量
| a |
| b |
点评:本题考查了向量垂直与数量积的关系、向量的投影的定义,考查了推理能力,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
不等式|x-1|+|x+2|≤a的解集非空,则实数a的取值范围是( )
| A、a>3 | B、a≥3 |
| C、a≤4 | D、a≥4 |
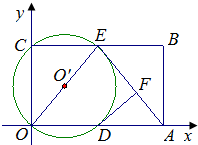 如图,在平面直角坐标系中,矩形ABCO的面积为24,边OA比OC大5.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为24,边OA比OC大5.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.