题目内容
已知命题p：方程
+
=1表示双曲线；命题q：不等式x2+ax+2＜0有解，若p∨q和￢q均为真命题，求实数a的取值范围．
| x2 |
| a+3 |
| y2 |
| a-1 |
考点：复合命题的真假
专题：圆锥曲线的定义、性质与方程,简易逻辑
分析：先求出命题p，q下的a的取值范围，再根据p∨q，￢q都为真命题，从而得到p真q假，所以求出p真时a的取值范围，q假时a的取值范围再求交集即可．
解答：
解：命题p：方程
+
=1表示双曲线，则（a+3）（a-1）＜0，解得-3＜a＜1；
命题q：不等式x2+ax+2＜0有解，则△=a2-8＞0，解得a＜-2
，或a＞2
；
∵p∨q，￢q均为真命题，∴p真q假；
∴-3＜a＜1且-2
≤a≤2
，∴-2
≤a＜1；
∴实数a的取值范围为[-2
，1)．
| x2 |
| a+3 |
| y2 |
| a-1 |
命题q：不等式x2+ax+2＜0有解，则△=a2-8＞0，解得a＜-2
| 2 |
| 2 |
∵p∨q，￢q均为真命题，∴p真q假；
∴-3＜a＜1且-2
| 2 |
| 2 |
| 2 |
∴实数a的取值范围为[-2
| 2 |
点评：考查双曲线的标准方程，一元二次不等式的解和判别式△的关系，p∨q，￢q的真假和p，q真假的关系．
练习册系列答案
相关题目
阅读右侧程序框图，输出结果S的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
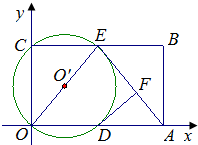如图，在平面直角坐标系中，矩形ABCO的面积为24，边OA比OC大5．E为BC的中点，以OE为直径的⊙O′交x轴于D点，过点D作DF⊥AE于点F．