题目内容
8.函数y=sin(x2)的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 先判断函数的奇偶性,再根据特殊值即可排除.
解答 解:因为y=f(-x)=sin(-x)2=sin(x2)=f(x),
所以y=f(x)为偶函数,
所以函数y=f(x)关于y轴对称,故排除A,C
当x=$\sqrt{π}$时,y=0,故排除B,
故选:D
点评 本题考查了函数图象的识别,关键是掌握函数的奇偶性和函数值得变化趋势,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.要得到函数$y=sin(\frac{π}{4}-3x)$的图象,只需要将函数y=sin3x的图象( )m.
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1(a>0)的一个焦点坐标为(2$\sqrt{3}$,0)则实数a的值为( )
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 16 | D. | 4 |
16.若实数x,y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{x>0}\\{y≤2}\end{array}\right.$,则$\frac{2y}{2x+1}$的取值范围是( )
| A. | [$\frac{4}{3}$,4] | B. | [$\frac{4}{3}$,4) | C. | [2,4] | D. | (2,4] |
20.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )
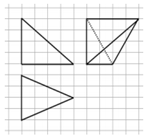

| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $2\sqrt{5}$ |
17.已知x,y∈R,满足x2+2xy+4y2=6,则z=x+y的取值范围为( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{6}$] | C. | [-$\sqrt{6}$,$\sqrt{6}$] | D. | [-$\sqrt{6}$,$\sqrt{2}$] |
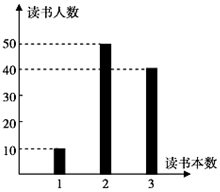 某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.