题目内容
10.直线l:y-1=k(x-1)和圆x2+y2-2x=0的位置关系是( )| A. | 相离 | B. | 相切或相交 | C. | 相交 | D. | 相切 |
分析 利用圆心到直线的距离与半径比较,大于半径,相离,等于则相切,小于则相交.
解答 解:由题意:圆心为(1,0),半径是1.
由直线l:y-1=k(x-1)知:直线过定点(1,1),
那么:圆心到定点的距离为d=1=r,说明定点在圆上;
∴过定点的直线必然与圆相切或相交.
故选B.
点评 本题考查了直线与圆的位置关系的判断方法.利用圆心到定点距离与半径比较,第二是消元,构造二次方程,利用判别式.属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
20.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )
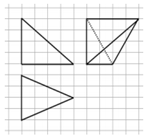

| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $2\sqrt{5}$ |
15.设全集U=R,集合A={x|x2-1<0},B={x|x(x-2)>0},则A∩(∁uB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
2.点P为直线$y=\frac{3}{4}x$上任一点,F1(-5,0),F2(5,0),则下列结论正确的是( )
| A. | ||PF1|-|PF2||>8 | B. | ||PF1|-|PF2||=8 | C. | ||PF1|-|PF2||<8 | D. | 以上都有可能 |
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$,若关于x的方程f(x)=k有三个不相等的实数根,则实数k的取值范围是( )
| A. | (-∞,-4) | B. | [-4,-3] | C. | (-4,-3] | D. | [-3,+∞) |
20.下列说法中,错误的一个是( )
| A. | 将23(10)化成二进位制数是10111(2) | |
| B. | 在空间坐标系点M(1,2,3)关于x轴的对称点为(1,-2,-3) | |
| C. | 数据:2,4,6,8的方差是数据:1,2,3,4的方差的2倍 | |
| D. | 若点A(-1,0)在圆x2+y2-mx+1=0的外部,则m>-2 |