题目内容
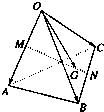 (B题)已知空间四边形OABC,M、N分别是对边OA、BC的中点,点G在线段MN上,且
(B题)已知空间四边形OABC,M、N分别是对边OA、BC的中点,点G在线段MN上,且| MG |
| GN |
| OG |
| OA |
| OB |
| OC |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用向量的三角形法则及平行四边形法则和向量形式的中点公式即可得出.
解答:
解:∵M、N分别是对边OA、BC的中点,
∴
=
,
=
(
+
).
∴
=
+
=
+
=
+
(
-
)=
+
=
+
+
,
因此x=
,y=z=
.
故选D.
∴
| OM |
| 1 |
| 2 |
| OA |
| ON |
| 1 |
| 2 |
| OB |
| OC |
∴
| OG |
| OM |
| MG |
| OM |
| 2 |
| 3 |
| MN |
| OM |
| 2 |
| 3 |
| ON |
| OM |
| 1 |
| 3 |
| OM |
| 2 |
| 3 |
| ON |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
因此x=
| 1 |
| 6 |
| 1 |
| 3 |
故选D.
点评:本题考查了向量的三角形法则及平行四边形法则,利用平面向量基本定理求系数.

练习册系列答案
相关题目
在△ABC中,(a+b+c)(a+b-c)=3ab,2cosAsinB=sinC,则△ABC的形状是( )
| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知函数y=f(x)在R上可导,满足 x•f′(x)+f(x)>0,则下列不等式一定成立的是( )
| A、2f(3)>3f(2) |
| B、2f(2)<3f(3) |
| C、2f(3)<3f(2) |
| D、2f(2)>3f(3) |
等差数列{an}中,S10=120,那么a5+a6的值是( )
| A、12 | B、24 | C、36 | D、48 |
在△ABC中若A=60°,B=45°,b=2
,则a为( )
| 2 |
A、2
| ||||
B、2
| ||||
C、
| ||||
| D、2 |
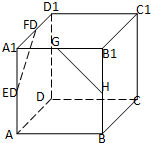 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是AA1,A1D1,A1B1,BB1的中点,则异面直线EF与GH所成的角的大小为( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是AA1,A1D1,A1B1,BB1的中点,则异面直线EF与GH所成的角的大小为( )| A、30° | B、45° |
| C、60° | D、120° |
用1,2,3,4这四个数字可排成必须含有重复数字的四位数有( )
| A、265个 | B、232个 |
| C、128个 | D、24个 |