已知△ABC中.A=$\frac{π}{2}$.a=2.b=$\sqrt{3}$.则B=( )A．$\frac{2π}{3}$B．$\frac{π}{3}$C．$\frac{π}{3}$或$\frac{2π}{3}$D．$\frac{π}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．已知△ABC中，A=$\frac{π}{2}$，a=2，b=$\sqrt{3}$，则B=（　　）

A．

$\frac{2π}{3}$

B．

$\frac{π}{3}$

C．

$\frac{π}{3}$或$\frac{2π}{3}$

D．

$\frac{π}{2}$

分析由已知及正弦定理可得sinB的值，利用大边对大角可求B为锐角，利用特殊角的三角函数值即可得解B的值．

解答解：∵A=$\frac{π}{2}$，a=2，b=$\sqrt{3}$，
∴由正弦定理可得：sinB=$\frac{b•sinA}{a}$=$\frac{\sqrt{3}×sin\frac{π}{2}}{2}$=$\frac{\sqrt{3}}{2}$，
∵b＜a，B为锐角，
∴B=$\frac{π}{3}$．
故选：B．

点评本题主要考查了正弦定理，大边对大角，特殊角的三角函数值在解三角形中的综合应用，考查了计算能力，属于基础题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

9．

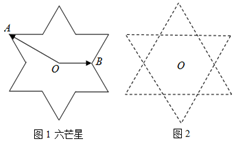如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（　　）

A．

[-4，4]

B．

$[{-\sqrt{21}，\sqrt{21}}]$

10．设a∈N^*，a＜28，则等式$（28-a）（29-a）…（35-a）=A_{35-a}^m$中m=8．

7．已知方程2x²-（m+1）x+m=0有两个不等正实根，则实数m的取值范围是（　　）

	A．	$0＜m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$		B．	$m＜3-2\sqrt{2}$或$m＞3+2\sqrt{2}$
	C．	$0＜m＜3-2\sqrt{2}$或$m＞3+2\sqrt{2}$		D．	$m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$

14．在△ABC中，（-$\sqrt{2}$a+b）cos C+ccos B=0，其中a，b，c分别是角A，B，C的对边．
（1）求C；
（2）若a=2，b=$\sqrt{2}$，求c．

4．已知数列{a_n}中，a₁=1，a_n+1=a_n+n+1，则数列$\{\frac{a_n}{n}\}$的前n项和为（　　）

A．

$\frac{{{n^2}+5n}}{2}$

B．

$\frac{{{n^2}+5n}}{4}$

C．

$\frac{{{n^2}+3n}}{2}$

D．

$\frac{{{n^2}+3n}}{4}$

11．设z=1-i（为虚数单位），则${z^2}+\frac{2}{z}$=（　　）

A．