题目内容
7.已知方程2x2-(m+1)x+m=0有两个不等正实根,则实数m的取值范围是( )| A. | $0<m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$ | B. | $m<3-2\sqrt{2}$或$m>3+2\sqrt{2}$ | ||
| C. | $0<m<3-2\sqrt{2}$或$m>3+2\sqrt{2}$ | D. | $m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$ |
分析 利用一元二次方程根的分布与系数的关系,二次函数的性质,可得△大于零,且两根之和、两根之积都大于零,从而求得m的范围.
解答 解:∵方程2x2-(m+1)x+m=0有两个不等正实根,∴△=(-m-1)2-8m>0,
即 m2-6m+1>0,求得m<3-2$\sqrt{2}$,或m>3+2$\sqrt{2}$.
再根据两根之和为$\frac{m+1}{4}$>0,且两根之积为$\frac{m}{2}$>0,求得m>0.
综合可得,0<m<3-2$\sqrt{2}$,或m>3+2$\sqrt{2}$,
故选:C.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
18.若i为虚数单位,设复数z满足|z|=1,则|z-1+i|的最大值为( )
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | 2+$\sqrt{2}$ |
19.已知△ABC中,A=$\frac{π}{2}$,a=2,b=$\sqrt{3}$,则B=( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
16.若$\left\{\begin{array}{l}{sinθ<0}\\{tanθ>0}\end{array}\right.$ 则角θ所在的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
17.在复平面中,下列复数中所对应的点在第三象限的是( )
| A. | -1+2i | B. | -1-2i | C. | 3+2i | D. | 3-2i |
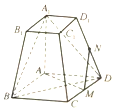 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.