题目内容
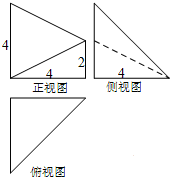已知某几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则此几何体的体积V=考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为四棱锥，画出其直观图，根据三视图的数据求底面面积与高，代入棱锥的体积公式计算．
解答：
解：由三视图知几何体为四棱锥，其直观图如图：
四棱锥的高为4，底面为直角梯形的面积S=
（2+4）×4=12，
∴几何体的体积V=
×12×4=16．
故答案为：16．
四棱锥的高为4，底面为直角梯形的面积S=
| 1 |
| 2 |
∴几何体的体积V=
| 1 |
| 3 |
故答案为：16．
点评：本题考查了由三视图求几何体的体积，解题的关键是由三视图判断几何体的形状及三视图的数据所对应的几何量．
练习册系列答案
相关题目
函数y=
+
的定义域为（ ）
| x(3-x) |
| x-1 |
| A、[0，3] |
| B、[1，3] |
| C、[1，+∞） |
| D、[3，+∞） |
已知函数y=
+
的单调递减区间是（
，6），则y的最大值是（ ）
| x-a |
| b-x |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |