题目内容
已知函数f(x)=x3+2x2.
(Ⅰ)求函数f(x)的极大值和极小值;
(Ⅱ)若不等式f(x)≥ax+4xlnx恒成立,求实数a的取值范围;
(Ⅲ)证明:
+
+
+…+
≥ln(n+1)(n∈N*).
(Ⅰ)求函数f(x)的极大值和极小值;
(Ⅱ)若不等式f(x)≥ax+4xlnx恒成立,求实数a的取值范围;
(Ⅲ)证明:
| 4×1+1 |
| 4×12 |
| 4×2+1 |
| 4×22 |
| 4×3+1 |
| 4×32 |
| 4×n+1 |
| 4×n2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)求出函数导函数f'(x),判断函数的单调性,然后求出极值.
(2)f(x)≥ax+4xlnx恒成立,转化为a≤x2+2x-4lnx对x∈(0,+∞)恒成立.通过函数的导数求出函数的最值即可.
(3)利用(2)知x>0时,x2+2x-4lnx≥3恒成立.推出
≥ln(n+1)-lnn,通过累加法证明所证明的不等式即可.
(2)f(x)≥ax+4xlnx恒成立,转化为a≤x2+2x-4lnx对x∈(0,+∞)恒成立.通过函数的导数求出函数的最值即可.
(3)利用(2)知x>0时,x2+2x-4lnx≥3恒成立.推出
| 4n+1 |
| 4×n2 |
解答:
解:(1)∵f'(x)=3x2+4x=x(3x+4),x(3x+4)>0
可得x∈(-∞,-
)和(0,+∞).
f(x)在(-∞,-
)和(0,+∞)上递增,在(-
,0)上递减
∴f(x)的极大值为f(-
)=
f(x)的极小值为f(0)=0.…(4分)
(2)f(x)≥ax+4xlnx恒成立,
即x3+2x2-4xlnx≥ax对?x∈(0,+∞)恒成立.
也即a≤x2+2x-4lnx对x∈(0,+∞)恒成立.
令g(x)=x2+2x-4lnx,只需a≤g(x)min即可.
g'(x)=2x+2-
=
,x∈(0,+∞),
y=g(x)在(0,1)上递减,(1,+∞)上递增
g(x)min=g(1)=3,∴a≤3.…(9分)
(3)由(2)知x>0时,x2+2x-4lnx≥3恒成立.
即(x-1)(x+3)≥4lnx 即
≥lnx恒成立.
令x=1+
得
≥ln(1+
),
即
≥ln(n+1)-lnn
故
≥lnn-ln(n-1)
…
≥ln3-ln2
≥ln2-ln1
把以上n个式子相加得
+
+
+…+
≥ln(n+1).…(14分)
可得x∈(-∞,-
| 4 |
| 3 |
f(x)在(-∞,-
| 4 |
| 3 |
| 4 |
| 3 |
∴f(x)的极大值为f(-
| 4 |
| 3 |
| 32 |
| 27 |
f(x)的极小值为f(0)=0.…(4分)
(2)f(x)≥ax+4xlnx恒成立,
即x3+2x2-4xlnx≥ax对?x∈(0,+∞)恒成立.
也即a≤x2+2x-4lnx对x∈(0,+∞)恒成立.
令g(x)=x2+2x-4lnx,只需a≤g(x)min即可.
g'(x)=2x+2-
| 4 |
| x |
| 2(x-1)(x+2) |
| x |
y=g(x)在(0,1)上递减,(1,+∞)上递增
g(x)min=g(1)=3,∴a≤3.…(9分)
(3)由(2)知x>0时,x2+2x-4lnx≥3恒成立.
即(x-1)(x+3)≥4lnx 即
| (x-1)(x+3) |
| 4 |
令x=1+
| 1 |
| n |
| 4n+1 |
| 4×n2 |
| 1 |
| n |
即
| 4n+1 |
| 4×n2 |
故
| 4(n-1)+1 |
| 4(n-1)2 |
…
| 4×2+1 |
| 4×22 |
| 4×1+1 |
| 4×12 |
把以上n个式子相加得
| 4×1+1 |
| 4×12 |
| 4×2+1 |
| 4×22 |
| 4×3+1 |
| 4×32 |
| 4×n+1 |
| 4×n2 |
点评:本题考查函数的导数的综合应用,函数的最值,构造法以及单调性的应用,难度比较大,是一个类型的常用方法.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
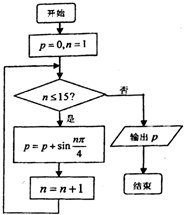
运行如图所示的程序框图后,输出的结果是( )

| A、0 | ||||
| B、1 | ||||
C、1+
| ||||
D、1+
|
已知a、b∈R,当x>0时,不等式ax+b≥lnx恒成立,则a+b的最小值为( )
| A、-1 | ||
| B、0 | ||
C、
| ||
| D、1 |
已知函数f(x+1)是偶函数,当x∈(1,+∞)时,函数f(x)=sinx-x,设a=f(-
),b=f(3),c=f(0),则a、b、c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<a<b |
| C、b<c<a |
| D、a<b<c |