题目内容
设函数f(x)=2cosxsin(x-
)+
sin2x+sinxcosx.
(1)求f(x)的最小正周期;
(2)设函数g(x)=f(
ωx+
(ω>0),g(
)=g(
)且g(x)在(
,
)上有最小值没有最大值,求ω的值.
| π |
| 3 |
| 3 |
(1)求f(x)的最小正周期;
(2)设函数g(x)=f(
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,三角函数的最值
专题:三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式整理,然后利用周期公式求得T.
(2)利用(1)中f(x)的解析式,求得g(x)的表达式,利用g(
)=g(
)推断出x=
为函数图象的一个对称轴,且根据已知为最小值,带入g(x)求得ω的表达式,最后根据g(x)在区间上有最小值没有最大值,判断出此区间小于半个周期,判断出ω的范围,最后求得ω.
(2)利用(1)中f(x)的解析式,求得g(x)的表达式,利用g(
| π |
| 6 |
| π |
| 3 |
| ||||
| 2 |
解答:
解:(1)f(x)=2cosxsin(x-
)+
sin2x+sinxcosx
=2cosx(
sinx-
cosx)+
sin2x+sinxcosx
=sinxcosx-
cos2x+
sin2x+sinxcosx
=2sinxcosx-
(cos2x-sin2x)
=sin2x-
cos2x
=2sin(2x-
),
∴T=
=π,
(2)g(x)=f(
ωx+
)=2sin(ωx+
-
)=2sin(ωx+
),
∵g(
)=g(
),
∴x=
=
,为函数g(x)的一个对称轴,
∵g(x)在(
,
)上有最小值没有最大值,
∴g(
)=2sin(
•ω+
)=-1,
∴
•ω+
=2kπ-
,则ω=8k-
,
∵g(x)在(
,
)上有最小值没有最大值,
∴
>
-
,即T>
,
∴
>
,
∴ω<6
∴对于ω=8k-
,k只能取到1,
即ω=
.
| π |
| 3 |
| 3 |
=2cosx(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=sinxcosx-
| 3 |
| 3 |
=2sinxcosx-
| 3 |
=sin2x-
| 3 |
=2sin(2x-
| π |
| 3 |
∴T=
| 2π |
| 2 |
(2)g(x)=f(
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵g(
| π |
| 6 |
| π |
| 3 |
∴x=
| ||||
| 2 |
| π |
| 4 |
∵g(x)在(
| π |
| 6 |
| π |
| 3 |
∴g(
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
∴
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| 10 |
| 3 |
∵g(x)在(
| π |
| 6 |
| π |
| 3 |
∴
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
∴
| 2π |
| ω |
| π |
| 3 |
∴ω<6
∴对于ω=8k-
| 10 |
| 3 |
即ω=
| 14 |
| 3 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.第二步一定要结合三角函数的图象去理解.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
与1303°终边相同的角是( )
| A、763° | B、493° |
| C、-137° | D、-47° |
已知复数
=b+i(a,b∈R,i为虚数单位),则a-2b=( )
| a-2i |
| i |
| A、1 | B、2 | C、3 | D、4 |
函数f(x)=(x2-1)cos2x在区间[0,2π]上的零点个数为( )
| A、6 | B、5 | C、4 | D、3 |
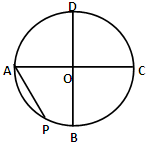 如图,圆O的半径为1,AC⊥BD,动点P从点A出发,沿圆弧
如图,圆O的半径为1,AC⊥BD,动点P从点A出发,沿圆弧
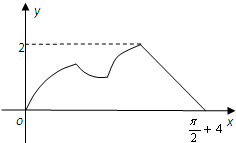


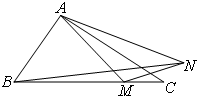 如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).
如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).