题目内容
设T(x)=|2x-1|,若不等式|a|T(x)≥|a+1|-|2a-1|对任意实数a≠0恒成立,则x的取值范围是( )
| A、(-∞,-1]∪[2,+∞) |
| B、(-∞,0]∪[1,+∞) |
| C、[0,1] |
| D、[-1,2] |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:依题意,可得|2x-1|≥
-
=|1+
|-|2-
|,令g(a)=|1+
|-|2-
|,利用绝对值不等式可得g(a)max=3,于是解不等式|2x-1|≥3即可得到答案.
| |a+1| |
| |a| |
| |2a-1| |
| |a| |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
解答:
解:∵T(x)=|2x-1|,
∴|a||2x-1|≥|a+1|-|2a-1|,又a≠0,
∴|2x-1|≥
-
=|1+
|-|2-
|,
令g(a)=|1+
|-|2-
|,
则g(a)≤|1+
+2-
|=3,即g(a)max=3,
∴|2x-1|≥3,即2x-1≥3或2x-1≤-3,
解得:x≥2或x≤-1.
∴x的取值范围是(-∞,-1]∪[2,+∞).
故选:A.
∴|a||2x-1|≥|a+1|-|2a-1|,又a≠0,
∴|2x-1|≥
| |a+1| |
| |a| |
| |2a-1| |
| |a| |
| 1 |
| a |
| 1 |
| a |
令g(a)=|1+
| 1 |
| a |
| 1 |
| a |
则g(a)≤|1+
| 1 |
| a |
| 1 |
| a |
∴|2x-1|≥3,即2x-1≥3或2x-1≤-3,
解得:x≥2或x≤-1.
∴x的取值范围是(-∞,-1]∪[2,+∞).
故选:A.
点评:本题考查绝对值不等式的解法,考查等价转化思想与构造函数思想,考查恒成立问题,属于中档题.

练习册系列答案
相关题目
点(0,5)到直线2x-y=0的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=(
)x-log2x,若x0是函数y=f(x)的零点,则当0<x<x0时,函数f(x)( )
| 1 |
| 5 |
| A、恒为正值 | B、等于0 |
| C、恒为负值 | D、不大于0 |
与1303°终边相同的角是( )
| A、763° | B、493° |
| C、-137° | D、-47° |
已知直线l1:2(m+1)x+(m-3)y+7-5m=0和l2:(m-3)x+2y-5=0,若l1⊥l2,则( )
| A、m=-2 | B、m=3 |
| C、m=-1或3 | D、m=3或-2 |
已知复数
=b+i(a,b∈R,i为虚数单位),则a-2b=( )
| a-2i |
| i |
| A、1 | B、2 | C、3 | D、4 |
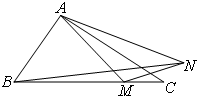 如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).
如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).