题目内容
函数y=（
）1-x的单调递增区间是 ．
| 1 |
| 2 |
考点：指数型复合函数的性质及应用
专题：函数的性质及应用
分析：根据复合函数单调性之间的关系即可得到结论．
解答：
解：∵y=（
）1-x=2x-1，
∴设t=x-1，则y=2t，
则函数t=x-1，y=2t，在各种的定义域上都是增函数，
∴y=（
）1-x=2x-1在R上也是单调递增，
即函数的递增区间为（-∞，+∞），
故答案为：（-∞，+∞）
| 1 |
| 2 |
∴设t=x-1，则y=2t，
则函数t=x-1，y=2t，在各种的定义域上都是增函数，
∴y=（
| 1 |
| 2 |
即函数的递增区间为（-∞，+∞），
故答案为：（-∞，+∞）
点评：本题主要考查复合函数的单调性的判定，利用指数函数的单调性的性质是解决本题的关键．
练习册系列答案
相关题目
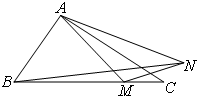如图已知△ABC中，AB=1，AC=2，∠BAC=120°，点M是边BC上的动点，动点N满足∠MAN=30°（点A，M，N按逆时针方向排列）．
三棱锥P-ABC的三视图如图所示，其中P是直角顶点．设M是面ABC内一点．定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（6，x，y），且