题目内容
已知函数f(x)=|x2-1|+x2+ax,若函数f(x)在区间(0,2)上有两个不同的零点x1,x2,求
+
的取值范围.
| 1 |
| x1 |
| 1 |
| x2 |
考点:函数的零点与方程根的关系
专题:常规题型,函数的性质及应用
分析:先根据函数f(x)在区间(0,2)上有两个不同的零点x1,x2,判断出0<x1<1,1<x2<2,然后分别把x1、x2代入表达式,消去参数a,整理出
+
形式就可以求出范围.
| 1 |
| x1 |
| 1 |
| x2 |
解答:
解:∵x1,x2是函数f(x)的两个零点,不妨设x1<x2,
f(x)=|x2-1|+x2+ax=
,
①若1<x1<x2<2,即在(0,1)上没有零点,
要使f(x)在(0,1)上没有零点,则须1+a>0,即a>-1,
这时,函数f(x)在(1,2)上也没有零点;
所以函数f(x)两个零点不可能都在(1,2)上;
②在(0,1)是一次函数,函数f(x)不可能有两个零点.
所必有0<x1<1,1<x2<2,
所以1+ax1=0,2x22+ax2-1=0
由以上两式消去a得,2x22-
-1=0
变形得:
+
=2x2
∵1<x2<2,
∴2<2x2<4,
∴
+
的取值范围是(2,4).
f(x)=|x2-1|+x2+ax=
|
①若1<x1<x2<2,即在(0,1)上没有零点,
要使f(x)在(0,1)上没有零点,则须1+a>0,即a>-1,
这时,函数f(x)在(1,2)上也没有零点;
所以函数f(x)两个零点不可能都在(1,2)上;
②在(0,1)是一次函数,函数f(x)不可能有两个零点.
所必有0<x1<1,1<x2<2,
所以1+ax1=0,2x22+ax2-1=0
由以上两式消去a得,2x22-
| x2 |
| x1 |
变形得:
| 1 |
| x1 |
| 1 |
| x2 |
∵1<x2<2,
∴2<2x2<4,
∴
| 1 |
| x1 |
| 1 |
| x2 |
点评:本题的难度较大,题目的突破口不好找,解决本题的关键是①判断x1,x2的取值范围;②对表达式进行适当的变形.

练习册系列答案
相关题目
已知复数
=b+i(a,b∈R,i为虚数单位),则a-2b=( )
| a-2i |
| i |
| A、1 | B、2 | C、3 | D、4 |
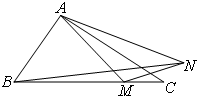 如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).
如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).