题目内容
已知直线l过点A（6，1）与圆C：x2+y2-8x+6y+21=0相切，
（1）求该圆的圆心坐标及半径长；
（2）求直线l的方程．
（1）求该圆的圆心坐标及半径长；
（2）求直线l的方程．
考点：直线和圆的方程的应用
专题：计算题,直线与圆
分析：（1）圆的方程化为标准方程，可得圆的圆心坐标及半径长；
（2）分类讨论，利用圆心到直线的距离等于半径，即可求直线l的方程．
（2）分类讨论，利用圆心到直线的距离等于半径，即可求直线l的方程．
解答：
解：（1）圆x2+y2-8x+6y+21=0，可得圆（x-4）2+（y+3）2=4，
所以圆心坐标为（4，-3），半径r=2．
（2）当直线l的斜率存在时，设直线l的方程为y-1=k（x-6），
即kx-y-6k+1=0，
则圆心到此直线的距离为d=
=
=2．
由此解得k=
，此时方程为3x-4y-14=0，
当直线l斜率不存在时，方程为x=6，
故直线l的方程为：3x-4y-14=0或x=6．
所以圆心坐标为（4，-3），半径r=2．
（2）当直线l的斜率存在时，设直线l的方程为y-1=k（x-6），
即kx-y-6k+1=0，
则圆心到此直线的距离为d=
| |4k+3-6k+1| | ||
|
| 2|k-2| | ||
|
由此解得k=
| 3 |
| 4 |
当直线l斜率不存在时，方程为x=6，
故直线l的方程为：3x-4y-14=0或x=6．
点评：本题考查圆的方程，考查直线与圆的位置关系，考查学生的计算能力，正确运用点到直线的距离公式是关键．
练习册系列答案
备战中考寒假系列答案
相关题目
过两点A（4，y），B（2，-3）的直线的倾斜角是135°，则y=（ ）
| A、5 | B、-5 | C、1 | D、-1 |
在△ABC中，若sinAcosB=cosAsinB，则△ABC为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
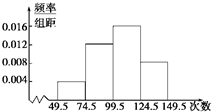春暖花开季节，某校举行了踢毽子比赛，将所得数据整理后，画出频率分布直方图如图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5．