题目内容

设等差数列{an}的前n项和为Sn，若a2a4a6a8=120，且
1
a4a6a8
+
1
a2a6a8
+
1
a2a4a8
+
1
a2a4a6
=
7
60
，则S9的值为
 
．
考点：等差数列的性质
专题：等差数列与等比数列
分析：由已知式子通分化简可得a5的值，而求和公式和性质可得S9=9a5，代入计算可得．
解答： 解：通分可得
1
a4a6a8
+
1
a2a6a8
+
1
a2a4a8
+
1
a2a4a6

=
a2
a2a4a6a8
+
a4
a2a4a6a8
+
a6
a2a4a6a8
+
a8
a2a4a6a8

=
a2+a4+a6+a8
a2a4a6a8
=
a2+a4+a6+a8
120
，
又∵a2+a8=a4+a6=2a5，
∴
a2+a4+a6+a8
120
=
4a5
120
=
7
60
，解得a5=
7
2
，
∴S9=
9(a1+a9)
2
=
9×2a5
2
=9a5=
63
2

故答案为：
63
2
点评：本题考查等差数列的性质和求和公式，划归为a5是解决问题的关键，属中档题．
练习册系列答案
相关题目
在△ABC中，若sinAcosB=cosAsinB，则△ABC为（　　）
A、直角三角形
B、等腰三角形
C、等腰直角三角形
D、等腰三角形或直角三角形
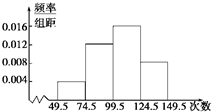春暖花开季节，某校举行了踢毽子比赛，将所得数据整理后，画出频率分布直方图如图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5．
（1）求第四小组的频率；
（2）参加这次比赛的学生人数是多少？
（3）在这次比赛中，学生踢毽子的中位数落在第几小组内？
已知：a+b+c=1，a，b，c＞0．
（1）求证：abc≤
1
27
；
（2）求证：a2+b2+c2≥
3abc
．
如图，射线OA，OB与x轴正半轴的夹角分别为45°和30°，过点P（1，0）的直线l分别交OA，OB于点A，B．
（1）当线段AB的中点为P时，求l的方程；
（2）当线段AB的中点在直线y=
x
2
上时，求l的方程．
椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点，则椭圆的离心率为
 
．
∫
π
-π
sin23xdx=
 
．
已知角α的终边经过点（3，-4），则sinα+cosα的值为
 
．
若i为虚数单位，m，n∈R，且
m+2i
i
=n+i，则mn=（　　）
A、-2B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网