题目内容
在平面直角坐标系xoy中,以O为圆心的圆与直线x-
y=4相切.
(1)求圆O的方程;
(2)已知圆C:x2+y2+2x-4y+3=0,判断它与圆O的位置关系,若相切求切线方程;若相交求相交弦所在的直线方程.
| 3 |
(1)求圆O的方程;
(2)已知圆C:x2+y2+2x-4y+3=0,判断它与圆O的位置关系,若相切求切线方程;若相交求相交弦所在的直线方程.
考点:圆的切线方程
专题:直线与圆
分析:(1)以O为圆心的圆与直线x-
y=4相切.则圆心到直线的距离等于半径.从而可得到圆的标准方程.
(2)将圆C:x2+y2+2x-4y+3=0的方程化为标准方程.根据两圆的圆心距与半径之间的关系即可判断两圆的位置关系为相交.两圆方程相减可得相交弦所在的直线方程.
| 3 |
(2)将圆C:x2+y2+2x-4y+3=0的方程化为标准方程.根据两圆的圆心距与半径之间的关系即可判断两圆的位置关系为相交.两圆方程相减可得相交弦所在的直线方程.
解答:
解:(1)∵圆O与直线x-
y=4相切,
∴圆心到直线的距离d=r.
∴r=
=2.
∴圆O的方程为:x2+y2=4.
(2)由(1)知,
圆心O(0,0),半径r1=2.
将圆C:x2+y2+2x-4y+3=0化为标准方程,
得(x+1)2+(y-2)2=2.
∴圆心C(-1,2),半径r2=
.
则圆心距|OC|=
.
r1+r2=2+
,
r1-r2=2-
.
∴2-
<
<2+
.
∴圆O与圆C相交.
圆O的方程x2+y2=4与圆C的方程x2+y2+2x-4y+3=0相减,
得2x-4y+7=0.
∴相交弦所在的直线方程为:2x-4y+7=0.
| 3 |
∴圆心到直线的距离d=r.
∴r=
| 4 | ||
|
∴圆O的方程为:x2+y2=4.
(2)由(1)知,
圆心O(0,0),半径r1=2.
将圆C:x2+y2+2x-4y+3=0化为标准方程,
得(x+1)2+(y-2)2=2.
∴圆心C(-1,2),半径r2=
| 2 |
则圆心距|OC|=
| 5 |
r1+r2=2+
| 2 |
r1-r2=2-
| 2 |
∴2-
| 2 |
| 5 |
| 2 |
∴圆O与圆C相交.
圆O的方程x2+y2=4与圆C的方程x2+y2+2x-4y+3=0相减,
得2x-4y+7=0.
∴相交弦所在的直线方程为:2x-4y+7=0.
点评:本题考查直线与圆相切的性质,直线与圆的位置关系的判断,相交弦所在的直线方程等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
y=-3与y=sin3x的交点个数是( )
| A、0 | B、1 | C、2 | D、无数个 |
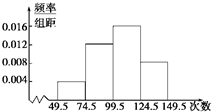 春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5. 如图,射线OA,OB与x轴正半轴的夹角分别为45°和30°,过点P(1,0)的直线l分别交OA,OB于点A,B.
如图,射线OA,OB与x轴正半轴的夹角分别为45°和30°,过点P(1,0)的直线l分别交OA,OB于点A,B.