题目内容
已知f（x）=ax2+2，若f′（1）=4，则a= ．
考点：导数的运算
专题：导数的概念及应用
分析：直接求出函数的导数，令x=1，建立关于a的方程，即可解得．
解答：
解：∵f（x）=ax2+2，
∴f'（x）=2ax2，
∴f'（1）=2a=4．
解得a=2．
故答案为：2
∴f'（x）=2ax2，
∴f'（1）=2a=4．
解得a=2．
故答案为：2
点评：本题主要考查导数的计算和求值，属于基础题．
练习册系列答案
相关题目
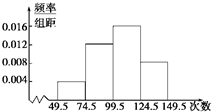春暖花开季节，某校举行了踢毽子比赛，将所得数据整理后，画出频率分布直方图如图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5．若i为虚数单位，m，n∈R，且
=n+i，则mn=（ ）
| m+2i |
| i |
| A、-2 | B、1 | C、2 | D、3 |
函数f（x）=2cosx对于x∈R，都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值为（ ）
A、
| ||
B、
| ||
| C、π | ||
| D、2π |