题目内容
已知a为实常数,函数f(x)=lnx-ax+1.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个不同的零点x1,x2(x1<x2).
(ⅰ)求实数a的取值范围;
(ⅱ)求证:
<x1<1,且x1+x2>2.(注:e为自然对数的底数)
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个不同的零点x1,x2(x1<x2).
(ⅰ)求实数a的取值范围;
(ⅱ)求证:
| 1 |
| e |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)写出函数f(x)的定义域,求出f'(x),分a≤0,a>0两种情况讨论,通过解不等式f'(x)>0,f'(x)<0可得单调区间;
(Ⅱ)(ⅰ)由(Ⅰ)可知,当a≤0时f(x)单调,不存在两个零点;当a>0时,可求得f(x)有唯一极大值,令其大于零,可得a的范围,再判断极大值点左右两侧附近的函数值小于零即可;(ⅱ)由(i)知可判断f(x)的单调性,根据零点存在定理可判断
<x1<1;分析:由0<x1<
,得
-x1>
,故只要证明:f(
-x1)>0就可以得出结论.下面给出证明:构造函数:g(x)=f(
-x)-f(x)=ln(
-x)-a(
-x)-(lnx-ax)(0<x≤
),利用导数可判断g(x)在区间(0,
]上为减函数,从而可得g(x1)>g(
)=0,再由f(x1)=0可得结论;
(Ⅱ)(ⅰ)由(Ⅰ)可知,当a≤0时f(x)单调,不存在两个零点;当a>0时,可求得f(x)有唯一极大值,令其大于零,可得a的范围,再判断极大值点左右两侧附近的函数值小于零即可;(ⅱ)由(i)知可判断f(x)的单调性,根据零点存在定理可判断
| 1 |
| e |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
解答:
解:(Ⅰ)f(x)的定义域为(0,+∞),其导数f'(x)=
-a.
①当a≤0时,f'(x)>0,函数在(0,+∞)上是增函数;
②当a>0时,在区间(0,
)上,f'(x)>0;在区间(
,+∞)上,f'(x)<0.
∴f(x)在(0,
)是增函数,在(
,+∞)是减函数.
(Ⅱ)(ⅰ)由(Ⅰ)知,当a≤0时,函数f(x)在(0,+∞)上是增函数,不可能有两个零点,
当a>0时,f(x)在(0,
)上是增函数,在(
,+∞)上是减函数,此时f(
)为函数f(x)的最大值,
当f(
)≤0时,f(x)最多有一个零点,∴f(
)=ln
>0,解得0<a<1,
此时,
<
<
,且f(
)=-1-
+1=-
<0,
f(
)=2-2lna-
+1=3-2lna-
(0<a<1),
令F(a)=3-2lna-
,则F'(x)=-
+
=
>0,∴F(a)在(0,1)上单调递增,
∴F(a)<F(1)=3-e2<0,即f(
)<0,
∴a的取值范围是(0,1).
(ii)由(Ⅱ)(i)可知函数f(x)在(0,
)是增函数,在(
,+∞)是减函数.f(x)=lnx-ax+1,
∴f(
)=-1-
+1=-
<0,f(1)=1-a>0.故
<x1<1;
第二部分:分析:∵0<x1<
,∴
-x1>
.只要证明:f(
-x1)>0就可以得出结论.
下面给出证明:构造函数:g(x)=f(
-x)-f(x)=ln(
-x)-a(
-x)-(lnx-ax)(0<x≤
),
则g'(x)=
-
+2a=
<0,
函数g(x)在区间(0,
]上为减函数.0<x1<
,则g(x1)>g(
)=0,又f(x1)=0,
于是f(
-x1)=ln(
-x1)-a(
-x1)+1-f(x1)=g(x1)>0.又f(x2)=0,
由(1)可知x2>
-x1,即x1+x2>
>2.
| 1 |
| x |
①当a≤0时,f'(x)>0,函数在(0,+∞)上是增函数;
②当a>0时,在区间(0,
| 1 |
| a |
| 1 |
| a |
∴f(x)在(0,
| 1 |
| a |
| 1 |
| a |
(Ⅱ)(ⅰ)由(Ⅰ)知,当a≤0时,函数f(x)在(0,+∞)上是增函数,不可能有两个零点,
当a>0时,f(x)在(0,
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
当f(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
此时,
| 1 |
| e |
| 1 |
| a |
| e2 |
| a2 |
| 1 |
| e |
| a |
| e |
| a |
| e |
f(
| e2 |
| a2 |
| e2 |
| a |
| e2 |
| a |
令F(a)=3-2lna-
| e2 |
| a |
| 2 |
| a |
| e2 |
| a2 |
| e2-2a |
| a2 |
∴F(a)<F(1)=3-e2<0,即f(
| e2 |
| a2 |
∴a的取值范围是(0,1).
(ii)由(Ⅱ)(i)可知函数f(x)在(0,
| 1 |
| a |
| 1 |
| a |
∴f(
| 1 |
| e |
| a |
| e |
| a |
| e |
| 1 |
| e |
第二部分:分析:∵0<x1<
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 2 |
| a |
下面给出证明:构造函数:g(x)=f(
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 1 |
| a |
则g'(x)=
| 1 | ||
x-
|
| 1 |
| x |
2a(x-
| ||
x(x-
|
函数g(x)在区间(0,
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
于是f(
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
由(1)可知x2>
| 2 |
| a |
| 2 |
| a |
点评:本题考查利用导数研究函数的单调性、零点及不等式的证明等知识,考查学生综合运用知识分析解决问题的能力、推理论证能力,本题综合性强,能力要求较高.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知集合M={x|x2+2x-8>0},N=[2,3),则( )
| A、M⊆N |
| B、N⊆M |
| C、M∩N=(2,3) |
| D、M∪N=(-4,3) |
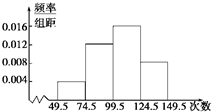 春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.