题目内容
已知x>-1,y>0且满足x+2y=1,则
+
的最小值为 .
| 1 |
| x+1 |
| 2 |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:由题意可得x+1>0,且(x+1)+2y=2,可得
+
=
(
+
)[(x+1)+2y]=
+
[
+
],由基本不等式可得.
| 1 |
| x+1 |
| 2 |
| y |
| 1 |
| 2 |
| 1 |
| x+1 |
| 2 |
| y |
| 5 |
| 2 |
| 1 |
| 2 |
| 2y |
| x+1 |
| 2(x+1) |
| y |
解答:
解:∵x>-1,y>0且满足x+2y=1,
∴x+1>0,且(x+1)+2y=2,
∴
+
=
(
+
)[(x+1)+2y]
=
+
[
+
]≥
+
×2
=
当且仅当
=
时取等号,
故
+
的最小值为:
故答案为:
∴x+1>0,且(x+1)+2y=2,
∴
| 1 |
| x+1 |
| 2 |
| y |
| 1 |
| 2 |
| 1 |
| x+1 |
| 2 |
| y |
=
| 5 |
| 2 |
| 1 |
| 2 |
| 2y |
| x+1 |
| 2(x+1) |
| y |
| 5 |
| 2 |
| 1 |
| 2 |
|
| 9 |
| 2 |
当且仅当
| 2y |
| x+1 |
| 2(x+1) |
| y |
故
| 1 |
| x+1 |
| 2 |
| y |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题考查基本不等式,1的代换是解决问题的关键,属基础题.

练习册系列答案
相关题目
过椭圆
+
=1(a>0)的焦点F作一直线交椭圆于P、Q两点,若线段PF、QF的长分别是p、q,则
+
=( )
| x2 |
| 4a2 |
| y2 |
| a2 |
| 1 |
| p |
| 1 |
| q |
A、
| ||
B、
| ||
| C、4a | ||
| D、2a |
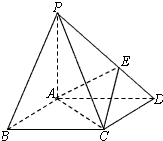 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=3,PB=PD=3
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=3,PB=PD=3