题目内容
直线l:y=kx+1与双曲线C:3x2-y2=3的右支交于不同的两点A、B.
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
考点:直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)将直线l的方程y=kx+1代入双曲线C的方程3x2-y2=3后,由题意知
,由此可知实数k的取值范围.
(Ⅱ)设A、B两点的坐标分别为(x1,y1)、(x2,y2),由题意:(x1-c)(x2-c)+y1y2=0,由此入手可求出k的值.
|
(Ⅱ)设A、B两点的坐标分别为(x1,y1)、(x2,y2),由题意:(x1-c)(x2-c)+y1y2=0,由此入手可求出k的值.
解答:
解:(Ⅰ)将直线l的方程y=kx+1代入双曲线C的方程3x2-y2=3,
整理得(3-k2)x2-2kx-4=0.
依题意,直线l与双曲线C的右支交于不同两点,
设两个交点的坐标分别为(x1,y1),(x2,y2),
∵(x1,y1),(x2,y2)都在双曲线C的右支,
x1>0,x2>0,
∴
解得k的取值范围是-2<k<-
.
(Ⅱ)假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0).
则由FA⊥FB得:(x1-c)(x2-c)+y1y2=0.
即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0.
整理得(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0.
化简得7k2+4k-11=0.
解得k=1或k=-
∵-2<k<-
,∴k=-
,使得以线段AB为直径的圆经过双曲线C的右焦点.
整理得(3-k2)x2-2kx-4=0.
依题意,直线l与双曲线C的右支交于不同两点,
设两个交点的坐标分别为(x1,y1),(x2,y2),
∵(x1,y1),(x2,y2)都在双曲线C的右支,
x1>0,x2>0,
∴
|
解得k的取值范围是-2<k<-
| 3 |
(Ⅱ)假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0).
则由FA⊥FB得:(x1-c)(x2-c)+y1y2=0.
即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0.
整理得(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0.
化简得7k2+4k-11=0.
解得k=1或k=-
| 11 |
| 7 |
∵-2<k<-
| 3 |
| 11 |
| 7 |
点评:本题主要考查直线、双曲线的方程和性质,曲线与方程的关系,及其综合应用能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
正方体ABCD-A′B′C′D′中,异面直线AB′和A′D所成角为( )
| A、45° | B、60° |
| C、90° | D、60°或120° |
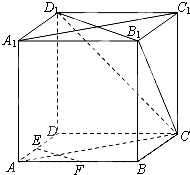 如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.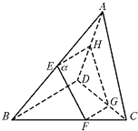 如图,空间四边形ABCD中,E、F、G分别是AB、BC、CD上,且满足AE:EB=CF:FB=2:1,CG:GD=3:1,过E、F、G的平面交AD于点H.
如图,空间四边形ABCD中,E、F、G分别是AB、BC、CD上,且满足AE:EB=CF:FB=2:1,CG:GD=3:1,过E、F、G的平面交AD于点H.