题目内容

若函数f（x）=2mcos2（
x
2
）+sinx的导函数的最大值等于
5
，则实数m的值等于
 
．
考点：导数的运算
专题：导数的概念及应用
分析：首先利用倍角公式化简解析式，然后根据其最大值求m．
解答： 解：由已知，f（x）=m+mcosx+sinx，
f′（x）=-msinx+cosx，所以它的最大值为
m2+1
=
5
，所以m=±2；
故答案为：±2．
点评：本题考查了三角函数的最值求法，属于基础题．
练习册系列答案
相关题目
极坐标方程ρsin2θ-2•cosθ=0表示的曲线是
 
．
在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，已知tanA+tanc=
5
4
（1-tanAtanC）．
（1）求sinB的值；
（2）若△ABC的面积为4，求BA•BC的值．
近年来，我国机动车拥有量呈现快速增加的趋势，可与之配套的基础设施建设速度相对迟缓，交通拥堵问题已经成为制约城市发展的重要因素，为了解某市的交通状况，现对其6条道路进行评估，得分分别为5、6、7、8、9、10规定评估的平均得分与全市的总体交通状况等级如下表：
评估的平均得分[0，6][6，8][8，10]
全市的总体交通不合格合格优秀
（1）求本次评估的平均得分，并参照上表估计该市的总体交通状况等级．
（2）用简单随机抽样方法从6条道路中抽取2条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过0.5的概率．
已知x＞-1，y＞0且满足x+2y=1，则
1
x+1
+
2
y
的最小值为
 
．
函数y=
3-x2
+
9
|x|+1
（　　）
A、只是偶函数
B、只是奇函数
C、既是偶函数，又是奇函数
D、是非奇非偶函数
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），离心率为
3
2
，两焦点分别为F1、F2，过F1的直线交椭圆C于M，N两点，且△F2MN的周长为8．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求过点（1，0）且斜率为
1
2
的线l被C所截线段的中点坐标．
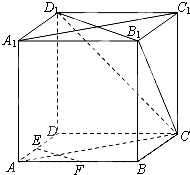如图，在正方体ABCD-A1B1C1D1中，E、F为棱AD、AB的中点．
（1）求证：平面CAA1C1⊥平面CB1D1；
（2）若正方体的棱长为2，求四边形EFB1D1的面积；
（3）求二面角B1-EF-C的余弦值（向量法除外）．
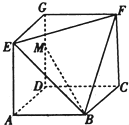已知几何体EFG-ABCD如图所示，其中四边形ABCD，CDGF，ADGE均为正方形，且边长为1，点M在边DG上．
（1）求证：BM⊥EF；
（2）是否存在点M，使得直线MB与平面BEF所成的角为45°．若存在，试求点M的位置．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网