题目内容

过椭圆
x2
4a2
+
y2
a2
=1（a＞0）的焦点F作一直线交椭圆于P、Q两点，若线段PF、QF的长分别是p、q，则
1
p
+
1
q
=（　　）
A、
4
a
B、
1
2a
C、4a
D、2a
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题意知
1
p
+
1
q
为定值，取PF=QF=p=q，得到
1
p
+
1
q
=
2
p
，将x=
3
a代入椭圆方程，求出p的值，从而得到答案．
解答： 解：由题意知
1
p
+
1
q
为定值，
不妨让直线⊥x轴，
则PF=QF=p=q，
那么
1
p
+
1
q
=
2
p
，
由
3a2
4a2
+
y2
a2
=1，
解得：y=±
a
2
，
∴p=
a
2
，
∴
1
p
+
1
q
=
2
p
=
4
a
，
故选：A．
点评：本题考查了椭圆的性质，特殊值法是选择题常用的方法之一，本题属于中档题．
练习册系列答案
相关题目
已知x＞-1，y＞0且满足x+2y=1，则
1
x+1
+
2
y
的最小值为
 
．
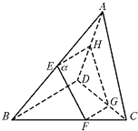如图，空间四边形ABCD中，E、F、G分别是AB、BC、CD上，且满足AE：EB=CF：FB=2：1，CG：GD=3：1，过E、F、G的平面交AD于点H．
（1）求AH：HD；
（2）求证：EH、FG、BD三线共点．
已知椭圆 C：
x2
a2
+
y2
b2
=1，（a＞b＞0）上一点P到它的两个焦点F1（左），F2（右）的距离的和是2
2
，短轴长为2
（1）求椭圆C的标准方程与离心率的值．
（2）若直线PF1的倾斜角为450，求直线PF1被椭圆C截的弦长的长度．
二元一次不等式Ax+By+C＞0表示的平面区域时直线Ax+By+C=0的上方区域．
 
（判断对错）
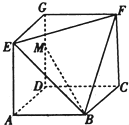已知几何体EFG-ABCD如图所示，其中四边形ABCD，CDGF，ADGE均为正方形，且边长为1，点M在边DG上．
（1）求证：BM⊥EF；
（2）是否存在点M，使得直线MB与平面BEF所成的角为45°．若存在，试求点M的位置．
线面角与二面角的取值范围分别是（　　）
A、[0，
π
2
），[0，π）
B、[0，
π
2
），[0，π]
C、[0，
π
2
]，[0，π）
D、[0，
π
2
]，[0，π]
已知函数f（x）=
(sinx-cosx)•sin2x
sinx
．
（1）求f（x）的定义域及最小正周期；
（2）若x∈（0，π），求f（x）的单调区间．
若方程cosx+cos（x+
π
3
）=
3
m3-2
3
有实根，则m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网