题目内容
已知动圆与⊙C1:(x+3)2+y2=9外切,且与⊙C2:(x-3)2+y2=1内切,求动圆圆心M的轨迹方程.
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:设动圆圆心M(x,y),半径为r,则|MC1|=r+3,|MC2|=r-1,可得|MC1|-|MC2|=r+3-r+1=4<|C1C2|=6,利用双曲线的定义,即可求动圆圆心M的轨迹方程.
解答:
解:设动圆圆心M的坐标为(x,y),半径为r,则|MC1|=r+3,|MC2|=r-1,
∴|MC1|-|MC2|=r+3-r+1=4<|C1C2|=6,
由双曲线的定义知,点M的轨迹是以C1、C2为焦点的双曲线的右支,且2a=4,a=2,
双曲线的方程为:
-
=1(x≥2).
∴|MC1|-|MC2|=r+3-r+1=4<|C1C2|=6,
由双曲线的定义知,点M的轨迹是以C1、C2为焦点的双曲线的右支,且2a=4,a=2,
双曲线的方程为:
| x2 |
| 4 |
| y2 |
| 5 |
点评:本题考查圆与圆的位置关系,考查双曲线的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、命题“?x≥0,x2+x-1<0”的否定是“?x0<0,x02+x0-1≥0” |
| C、命题“若x=y,则sin x=sin y”的逆否命题为假命题 |
| D、若“p∨q”为真命题,则p,q中至少有一个为真命题 |
已知抛物线:x2=-4y,直线l:x-y-1=0与抛物线交于A、B两点,则|AB|的长为( )
| A、6 | B、7 | C、8 | D、9 |
已知F1,F2是椭圆的左,右焦点,以右焦点F2为圆心的圆过F1且与右准线相切,则椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若椭圆
+y2=1与双曲线
-
=1 (a>0)有相同的焦点,则a=( )
| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
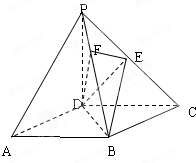 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.