题目内容
已知函数f(x)=
,则函数g(x)=f(t)-2在区间(-1,3]上的零点个数是
( )
|
( )
| A、1 | B、2 | C、3 | D、4 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:画出函数的图象,通过图象直接得出结论.
解答:
解:画出函数f(x)的图象,如图示:
 ,
,
令g(x)=0,即f(x)=2,
由图象得:x=1时,f(x)=2,
故函数g(x)有1个零点,
故选:A.
 ,
,令g(x)=0,即f(x)=2,
由图象得:x=1时,f(x)=2,
故函数g(x)有1个零点,
故选:A.
点评:本题考查了函数的零点问题,考查了分类讨论思想,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列椭圆的形状哪一个更圆( )
| A、9x2+y2=36 | ||||
B、
| ||||
| C、x2+9y2=36 | ||||
D、
|
已知椭圆
+
=1(a>b>0),过焦点F1的弦AB的长是2,另一焦点为F2,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
圆心角为1rad,半径为1的扇形的面积为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、π |
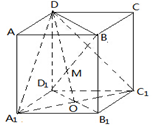 如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则
如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则