题目内容
已知a<b,若函数f(x),g(x)满足
f(x)dx=
g(x)dx,则称f(x),g(x)为区间[a,b]上的一组“等积分”函数,给出四组函数:
①f(x)=2|x|,g(x)=x+1;
②f(x)=sinx,g(x)=cosx;
③f(x)=
,g(x)=
πx2;
④函数f(x),g(x)分别是定义在[-1,1]上的奇函数且积分值存在.
其中为区间[-1,1]上的“等积分”函数的组数是( )
| ∫ | b a |
| ∫ | b a |
①f(x)=2|x|,g(x)=x+1;
②f(x)=sinx,g(x)=cosx;
③f(x)=
| 1-x2 |
| 3 |
| 4 |
④函数f(x),g(x)分别是定义在[-1,1]上的奇函数且积分值存在.
其中为区间[-1,1]上的“等积分”函数的组数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:微积分基本定理
专题:计算题,导数的概念及应用
分析:利用“等积分”函数的定义,对给出四组函数求解,即可得出区间[-1,1]上的“等积分”函数的组数
解答:
解:对于①,
f(x)dx=
2|x|dx=
2(-x)dx+
2xdx=2,而
g(x)dx=(
x2+x)
=2,所以①是一组“等积分”函数;
对于②,
f(x)dx=
sinxdx=0,而
g(x)dx=
cosxdx=2sin1≠0,所以②不是一组“等积分”函数;对于③,由于函数f(x)的图象是以原点为圆心,1为半径的半圆,故
f(x)dx=
dx=
,而
g(x)dx
πx3|
=
,所以③是一组“等积分”函数;
对于④,由于函数f(x),g(x)分别是定义在[-1,1]上的奇函数且积分值存在,利用奇函数的图象关于原点对称和定积分的几何意义,可以求得函数的定积分
f(x)dx=
g(x)dx=0,所以④是一组“等积分”函数,
故选C.
| ∫ | 1 -1 |
| ∫ | 1 -1 |
| ∫ | 0 -1 |
| ∫ | 1 0 |
| ∫ | 1 -1 |
| 1 |
| 2 |
| | | 1 -1 |
对于②,
| ∫ | 1 -1 |
| ∫ | 1 -1 |
| ∫ | 1 -1 |
| ∫ | 1 -1 |
| ∫ | 1 -1 |
| ∫ | 1 -1 |
| 1-x2 |
| π |
| 2 |
| ∫ | 1 -1 |
| 1 |
| 4 |
1 -1 |
| π |
| 2 |
对于④,由于函数f(x),g(x)分别是定义在[-1,1]上的奇函数且积分值存在,利用奇函数的图象关于原点对称和定积分的几何意义,可以求得函数的定积分
| ∫ | 1 -1 |
| ∫ | 1 -1 |
故选C.
点评:本题考查“等积分”函数,考查定积分的计算,有点复杂.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
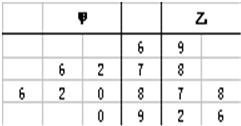 如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )
如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分比乙同学平均分高;
③甲同学成绩的平均分比乙同学平均分低;
④甲同学成绩的方差小于乙同学成绩的方差.
| A、①③ | B、①②④ | C、③④ | D、③ |