题目内容
经过双曲线的一个焦点作垂直于实轴的直线,交双曲线与A,B两点,交双曲线的渐近线于P,Q两点,若|PQ|=2|AB|,则双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出双曲线方程,求其渐近线方程,令x=c,解出|PQ|,|AB|,从而求离心率.
解答:
解:不妨设双曲线的方程为
-
=1,
令x=c,解得,y=±
,
∴|AB|=2
,
又∵双曲线
-
=1的渐近线方程为y=±
x,
令x=c,解得,y=±
c,
∴|PQ|=2
c,
又∵|PQ|=2|AB|,
∴2
c=4
,即c=2b,
∴a=
b,
∴e=
=
=
,
故选D.
| x2 |
| a2 |
| y2 |
| b2 |
令x=c,解得,y=±
| b2 |
| a |
∴|AB|=2
| b2 |
| a |
又∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
令x=c,解得,y=±
| b |
| a |
∴|PQ|=2
| b |
| a |
又∵|PQ|=2|AB|,
∴2
| b |
| a |
| b2 |
| a |
∴a=
| 3 |
∴e=
| c |
| a |
| 2b | ||
|
2
| ||
| 3 |
故选D.
点评:本题考查了双曲线的简单性质,思路比较简单,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆
+
=1(a>b>0),过焦点F1的弦AB的长是2,另一焦点为F2,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
圆心角为1rad,半径为1的扇形的面积为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、π |
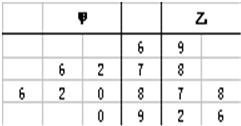 如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )
如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )