题目内容
若椭圆
+y2=1与双曲线
-
=1 (a>0)有相同的焦点,则a=( )
| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆方程的c2=4-1=3,再求双曲线方程的为a2+2,再由已知得到方程,解出a即可.
解答:
解:椭圆
+y2=1的c2=4-1=3,
由于椭圆
+y2=1与双曲线
-
=1 (a>0)有相同的焦点,
则a2+2=3,
解得a=1,
故选A.
| x2 |
| 4 |
由于椭圆
| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| 2 |
则a2+2=3,
解得a=1,
故选A.
点评:本题考查椭圆和双曲线的方程和性质,注意椭圆与双曲线的a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知不等式ax2+bx-2>0的解集是{x|-2<x<-
},则a-b的值为( )
| 1 |
| 4 |
| A、2 | B、3 | C、4 | D、5 |
已知椭圆
+
=1(a>b>0),过焦点F1的弦AB的长是2,另一焦点为F2,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
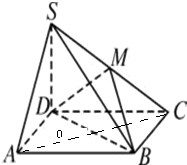 如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.
如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.