题目内容
已知抛物线:x2=-4y,直线l:x-y-1=0与抛物线交于A、B两点,则|AB|的长为( )
| A、6 | B、7 | C、8 | D、9 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:x2=-4y且x-y-1=0,转化为二次方程,利用弦长公式求解.
解答:
解:设A(x1,y1),B(x2,y2)
∵抛物线:x2=-4y,直线l:x-y-1=0与抛物线交于A、B两点
∴
,化简得:x2+4x-4=0,
根据韦达定理得:x1+x2=-4,x1x2=-4,
∴|AB|=
|x1-x2|=
=8,
故选:C
∵抛物线:x2=-4y,直线l:x-y-1=0与抛物线交于A、B两点
∴
|
根据韦达定理得:x1+x2=-4,x1x2=-4,
∴|AB|=
| 1+1 |
| 2 |
| 42-4(-4) |
故选:C
点评:本题综合考查了方程的方法,解决抛物线与直线的位置关系,充分运用了弦长公式,解决问题.

练习册系列答案
相关题目
下列椭圆的形状哪一个更圆( )
| A、9x2+y2=36 | ||||
B、
| ||||
| C、x2+9y2=36 | ||||
D、
|
已知椭圆
+
=1(a>b>0),过焦点F1的弦AB的长是2,另一焦点为F2,则△ABF2的周长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
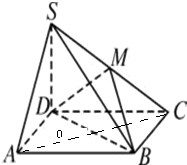 如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.
如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.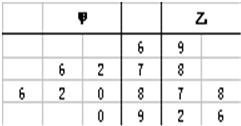 如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )
如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )