题目内容

1．已知偶函数f（x）在区间[0，+∞）上单调递增，则满足f（2x+1）＜f（5）的x的所在区间是（-3，2）．

分析 由f（x）为偶函数且在[0，+∞）上单调递增，便可由f（2x+1）＜f（5）得f（|2x+1|）＜f（5），解该绝对值不等式便可得出x的取值范围．

解答 解：∵f（x）为偶函数，
∴由f（2x+1）＜f（5）得f（|2x+1|）＜f（5）．
又f（x）在[0，+∞）上单调递增，
∴|2x+1|＜5，
解得-3＜x＜2，
∴x的取值范围是（-3，2）．
故答案为：（-3，2）．

点评 考查偶函数的定义，增函数的定义，根据函数单调性解不等式的方法，以及绝对值不等式的解法．

练习册系列答案
相关题目
11．已知圆${x^2}+{y^2}+（4-2a）x-2\sqrt{3}ay+4{a^2}-4a-12=0$，定直线l经过点A（1，0），若对任意的实数a，定直线l被圆C截得的弦长始终为定值d，求得此定值d等于（　　）
A．$2\sqrt{7}$B．$\sqrt{31}$C．$\sqrt{34}$D．$\sqrt{37}$
12．已知函数$f（x）=\frac{x}{{1+{x^2}}}$，x∈（0，1）．
（1）令x1，x2∈（0，1），证明：（x1-x2）•[f（x1）-f（x2）]≥0；
（2）若x∈（0，1）时，恒有$\frac{{3{x^2}-x}}{{1+{x^2}}}≥a（{x-\frac{1}{3}}）$，求a的值；
（3）若x1，x2，x3都是正数，且x1+x2+x3=1，求$y=\frac{{3x_1^2-{x_1}}}{1+x_1^2}+\frac{{3x_2^2-{x_2}}}{1+x_2^2}+\frac{{3x_3^2-{x_3}}}{1+x_3^2}$的最小值．
9．在区间[-2，3]上随机取一个数x，则x∈[-1，1]的概率是（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{1}{2}$D．$\frac{3}{5}$
16．已知x，y的取值如表所示，
x01234 
y2.33.94.65.1 6.6
从所得散点图分析，y与x线性相关，且$\widehat{y}$=0.98x+a，则a的值为（　　）
A．2.45B．2.54C．2.64D．3.04
6．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$，则z=x+2y的最小值为（　　）
A．0B．0.5C．2D．9
13．设全集A={1，2，3，4，5}，B={2，4，6，8，10}，则A∪B=（　　）
A．{2，4}B．{1，2，3，4，5，6，8，10}
C．{1，2，3，4，5}D．{2，4，6，8，10}
10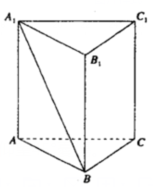．如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥面ABC，若AB=AA1，则直线A1B与AC所成角的余弦值为（　　）
A．$\frac{\sqrt{2}}{2}$B．$\frac{\sqrt{2}}{4}$C．$\frac{\sqrt{14}}{2}$D．$\frac{\sqrt{14}}{4}$
11．一个四棱锥的三视图如图所示，则这个四棱锥的体积等于（　　）
A．8B．4C．$\frac{8}{3}$D．$\frac{4}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网