题目内容
11.已知圆${x^2}+{y^2}+(4-2a)x-2\sqrt{3}ay+4{a^2}-4a-12=0$,定直线l经过点A(1,0),若对任意的实数a,定直线l被圆C截得的弦长始终为定值d,求得此定值d等于( )| A. | $2\sqrt{7}$ | B. | $\sqrt{31}$ | C. | $\sqrt{34}$ | D. | $\sqrt{37}$ |
分析 根据圆的方程求出圆心和半径,由题意可得圆心C到直线l的距离为定值.当直线l的斜率不存在时,经过检验不符合条件.当直线l的斜率存在时,直线l的方程为 y-0=k(x-1),圆心C到直线l的距离为定值,即可得出结论.
解答 解:圆C:${x^2}+{y^2}+(4-2a)x-2\sqrt{3}ay+4{a^2}-4a-12=0$ 即[x-(a-2)]2+(y-$\sqrt{3}a$)2=16,表示以C(a-2,$\sqrt{3}a$)为圆心,半径等于4的圆.
∵直线l经过点(1,0),对任意的实数m,定直线l被圆C截得的弦长为定值,则圆心C到直线l的距离为定值.
当直线l的斜率不存在时,直线l的方程为x=1,圆心C到直线l的距离为|a-2-1|=|a-3|,不是定值.
当直线l的斜率存在时,设直线l的斜率为k,则直线l的方程为 y-0=k(x-1),即 kx-y-k=0.
此时,圆心C到直线l的距离h=$\frac{|k(a-2)-\sqrt{3}a-k|}{\sqrt{{k}^{2}+1}}$为定值,与a无关,
故k=$\sqrt{3}$,h=$\frac{3\sqrt{3}}{2}$,
∴d=2$\sqrt{16-{(\frac{3\sqrt{3}}{2})}^{2}}$=$\sqrt{37}$,
故选:D
点评 本题主要考查圆的标准方程,直线和圆的位置关系,点到直线的距离公式,体现了分类讨论的数学思想,属于中档题

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
19.定积分${∫}_{0}^{2}$(-3)dx等于( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
16.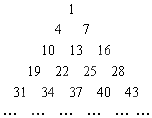 将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
 将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
将等差数列1,4,7…,按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )| A. | 571 | B. | 574 | C. | 577 | D. | 580 |
3.已知正六边形ABCDEF的边长为1,则$\overrightarrow{AB}•\overrightarrow{AC}$的值为( )
| A. | $-\frac{3}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{2}$ |