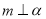题目内容
设函数f（x）=g（x）+x+lnx，曲线y=g（x）在点（1，g（1））处的切线方程为y=2x+1，则曲线y=f（x）在点（1，f（1））处的切线方程为（ ）
A.y=4x B.y=4x﹣8 C.y=2x+2 D.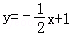
A
【解析】
试题分析：据曲线在切点处的导数值为曲线切线的斜率，求g′（1）进一步求出f′（1），由点斜式求出切线方程．
【解析】
由已知g′（1）=2，而
，
所以f′（1）=g′（1）+1+1=4，即切线斜率为4，
又g（1）=3，
故f（1）=g（1）+1+ln1=4，
故曲线y=f（x）在点（1，f（1））处的切线方程为y﹣4=4（x﹣1），即y=4x，
故选A．
练习册系列答案
同步练习强化拓展系列答案
相关题目
中，
，且对任意的正整数
都有
，则若
时，
_________.
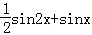，则f′（x）是（ ）
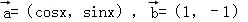，将函数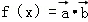
的图象按向量
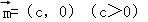平移后，所得图象恰好为函数y=﹣f′（x）（f′（x）为f（x）的导函数）的图象，则c的值可以为（ ）
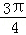B.π C.
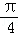D.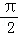
（sinx﹣cosx）的导函数为f′（x），则下列结论正确的是（ ）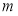
，
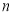是两条不同直线，
，
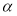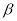是两个不同的平面，且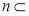
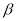，则下列叙述正确的是
，
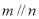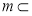
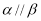
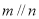
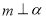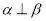
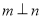，则
，则