题目内容
(2012•德阳三模)已知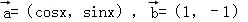 ,将函数
,将函数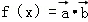 的图象按向量
的图象按向量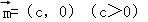 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
A.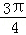 B.π C.
B.π C.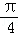 D.
D.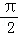
D
【解析】
试题分析:先根据辅助角公式进行化简,f(x)= cos(x+
cos(x+ ),按向量
),按向量 平移后得到y=
平移后得到y= cos(x﹣c+
cos(x﹣c+ )
)
的图象.由题意可得 cos(x﹣c+
cos(x﹣c+ )=
)= sin(x+
sin(x+ ),从而得到c的值.
),从而得到c的值.
【解析】
∵f(x)= =cosx﹣sinx=
=cosx﹣sinx= cos(x+
cos(x+ ),
),
把函数 的图象按向量
的图象按向量 平移后,
平移后,
所得图象对应的函数为y= cos(x﹣c+
cos(x﹣c+ ).
).
而﹣f′(x)= sin(x+
sin(x+ ),平移后,所得图象恰好为函数y=﹣f′(x),
),平移后,所得图象恰好为函数y=﹣f′(x),
故  cos(x﹣c+
cos(x﹣c+ )=
)= sin(x+
sin(x+ ),故可让c=
),故可让c= ,
,
故选 D.

练习册系列答案
相关题目
 +1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .
+1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .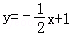
 等于( )
等于( ) 的导数是( )
的导数是( ) B.﹣sinx C.
B.﹣sinx C. D.
D.
 的图象大致为( )
的图象大致为( )