题目内容
判断函数y=
+1在区间(2,+∞)内的单调性.
| 1 |
| 2(x-2)2 |
考点:函数单调性的性质
专题:函数的性质及应用
分析:设t=2(x-2)2,利用换元法将函数转化为两个基本初等函数,然后利用复合函数的单调性之间的关系即可判断函数的单调性.
解答:
解:设t=2(x-2)2,则y=
,
当x∈(2,+∞)上,函数t=2(x-2)2单调递增且t>0,
∵y=
在t>0时,函数单调递减,
∴根据复合函数的单调性的性质可知 函数y=
+1在区间(2,+∞)内的单调递减.
| 1 |
| t |
当x∈(2,+∞)上,函数t=2(x-2)2单调递增且t>0,
∵y=
| 1 |
| t |
∴根据复合函数的单调性的性质可知 函数y=
| 1 |
| 2(x-2)2 |
点评:本题主要考查函数单调性的判断,利用换元法结合复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )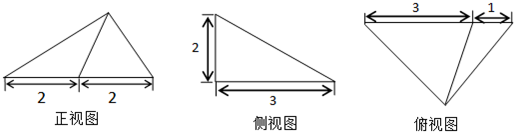

A、
| ||
| B、4 | ||
| C、2 | ||
D、
|