题目内容
下列命题正确的是( )
A、
| ||||||||
| B、对任意的实数x,都有x3≥x2-x+1恒成立. | ||||||||
C、y=
| ||||||||
| D、y=2x(2-x),(x≥2)的最大值为2 |
考点:命题的真假判断与应用
专题:不等式的解法及应用
分析:必须对选项一一加以判断:对A运用分析法考虑;对B应用作差法考虑;对C应用基本不等式考虑;对D应用二次函数的最值求得.
解答:
解:因为
+
<
+
?(
+
)2<(
+
)2?17+2
<17+2
?
<
?70<42,显然不成立,所以A错;
因为x3-(x2-x+1)=(x3-1)-(x2-x)=(x-1)(x2+x+1)-x(x-1)=(x-1)(x2+1),
所以对任意的实数x,x3-(x2-x+1)≥0不恒成立,只有x≥1,才恒成立,故B错;
因为y=
+x2=
+(x2+2)-2≥2
-2=4-2=2
当且仅当x=0时y取最小值2,所以C正确;
因为y=2x(2-x)=-2(x-1)2+2,当x≥2时,函数为减函数,x=2,y取最大值0,所以D错.
故选:C
| 7 |
| 10 |
| 3 |
| 14 |
| 7 |
| 10 |
| 3 |
| 14 |
| 70 |
| 42 |
?
| 70 |
| 42 |
因为x3-(x2-x+1)=(x3-1)-(x2-x)=(x-1)(x2+x+1)-x(x-1)=(x-1)(x2+1),
所以对任意的实数x,x3-(x2-x+1)≥0不恒成立,只有x≥1,才恒成立,故B错;
因为y=
| 4 |
| x2+2 |
| 4 |
| x2+2 |
|
当且仅当x=0时y取最小值2,所以C正确;
因为y=2x(2-x)=-2(x-1)2+2,当x≥2时,函数为减函数,x=2,y取最大值0,所以D错.
故选:C
点评:本题主要考查不等式的性质和应用,运用基本不等式求最值,注意一正二定三等,同时应掌握不等式证明的分析法和作差法,本题是一道中档题.

练习册系列答案
相关题目
命题“?x∈R,x2-3x+2≥0”的否定是( )
| A、?x∈R,x2-3x+2<0 |
| B、?x∈R,x2-3x+2>0 |
| C、?x∈R,x2-3x+2≤0 |
| D、?x∈R,x2-3x+2≥0 |
某几何体的三视图如图所示,则该几何体的体积是( )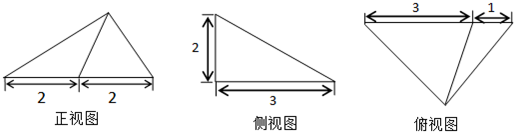

A、
| ||
| B、4 | ||
| C、2 | ||
D、
|
下列说法正确的是( )
| A、“p∨q为真”是“p∧q为真”的充分不必要条件 | ||||
| B、已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | ||||
C、若a,b∈[0,1],则不等式a2+b2<
| ||||
| D、已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
设A与B是相互独立事件,则下列命题正确的是( )
| A、A与B是互斥事件 | ||||
| B、A与B是对立事件 | ||||
C、
| ||||
D、
|
