题目内容
设直线y=ax+1(a>0)与曲线
=
恰有2个公共点,则a的取值的集合为 .
| lg(2-|x-1|) |
| lgy |
| 1 |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:利用
=
,推导出y=
,由此能推导出a的取值的集合.
| lg(2-|x-1|) |
| lgy |
| 1 |
| 2 |
|
解答:
解:∵
=
,
∴lgy=2lg(2-|x-1|)=lg(2-|x-1|)2,
且2-|x-1|>0,即-1<x<3.
∴y=(2-|x-1|)2=4-4|x-1|+(x-1)2,
∴y=
,
作出其图象,如右图:
∵y=ax+1(a>0)恒过点C(0,1),
直线y=ax+1(a>0)与曲线
=
恰有2个公共点,
∴直线y=ax+1(a>0)过A(-1,0),C(0,1)时,
amin→
=1;
直线y=ax+1(a>0)过D(1,4),C(0,1)时,
amax→
=3.
∴a的取值的集合为(1,3).
故答案为:(1,3)
| lg(2-|x-1|) |
| lgy |
| 1 |
| 2 |
∴lgy=2lg(2-|x-1|)=lg(2-|x-1|)2,

且2-|x-1|>0,即-1<x<3.
∴y=(2-|x-1|)2=4-4|x-1|+(x-1)2,
∴y=
|
作出其图象,如右图:
∵y=ax+1(a>0)恒过点C(0,1),
直线y=ax+1(a>0)与曲线
| lg(2-|x-1|) |
| lgy |
| 1 |
| 2 |
∴直线y=ax+1(a>0)过A(-1,0),C(0,1)时,
amin→
| 1-0 |
| 0+1 |
直线y=ax+1(a>0)过D(1,4),C(0,1)时,
amax→
| 4-1 |
| 1-0 |
∴a的取值的集合为(1,3).
故答案为:(1,3)
点评:本题考查函数的图象的应用,解题时要注意等价转化思想和数形结合思想的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )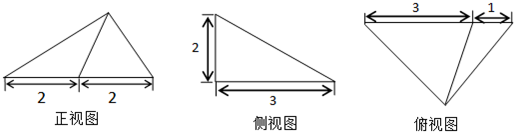

A、
| ||
| B、4 | ||
| C、2 | ||
D、
|