题目内容
已知f（x）=
的定义域为R，则k的取值范围是 ．
| x2+x+1 |
| kx2-kx+4 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由题意，kx2-kx+4≠0的解集为R，从而可对k讨论，即可求解．
解答：
解：由题意，kx2-kx+4≠0的解集为R
∴k=0时，成立，
k≠0时，△=k2-16k＜0，
∴0＜k＜16．
综上，k的取值范围是：0≤k＜16．
故答案为：[0，16）．
∴k=0时，成立，
k≠0时，△=k2-16k＜0，
∴0＜k＜16．
综上，k的取值范围是：0≤k＜16．
故答案为：[0，16）．
点评：本题以函数为依托，考查函数的性质，考查解不等式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
命题“?x∈R，x2-3x+2≥0”的否定是（ ）
| A、?x∈R，x2-3x+2＜0 |
| B、?x∈R，x2-3x+2＞0 |
| C、?x∈R，x2-3x+2≤0 |
| D、?x∈R，x2-3x+2≥0 |
某几何体的三视图如图所示，则该几何体的体积是（ ）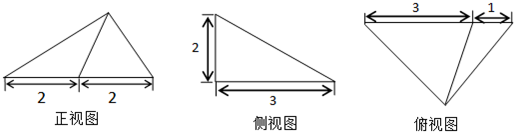
A、
| ||
| B、4 | ||
| C、2 | ||
D、
|