题目内容
记曲线y=sin
x,x∈[-3,1]与y=1所围成的封闭区域为D,若直线y=ax+2与D有公共点,则实数a的取值范围是( )
| π |
| 2 |
A、[-1,
| ||||
B、(-∞,-1]∪[
| ||||
C、[-
| ||||
D、(-∞,-
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:作出区域D,易知直线y=ax+2过定点A(0,2),斜率为a,由斜率公式数形结合可得.
解答:
 解:由题意封闭区域为D如图所示(阴影),
解:由题意封闭区域为D如图所示(阴影),
易知直线y=ax+2过定点A(0,2),斜率为a,
又可得B(-3,1),C(1,1),
由斜率公式可得kAB=
=
,kAC=
=-1,
易得满足题意得直线介于AB和AC之间,
故实数a的取值范围是(-∞,-1]∪[
,+∞)
故选:B
 解:由题意封闭区域为D如图所示(阴影),
解:由题意封闭区域为D如图所示(阴影),易知直线y=ax+2过定点A(0,2),斜率为a,
又可得B(-3,1),C(1,1),
由斜率公式可得kAB=
| 2-1 |
| 0-(-3) |
| 1 |
| 3 |
| 2-1 |
| 0-1 |
易得满足题意得直线介于AB和AC之间,
故实数a的取值范围是(-∞,-1]∪[
| 1 |
| 3 |
故选:B
点评:本题考查正弦函数的图象,涉及直线的斜率和斜率公式,数形结合是解决问题的关键,属中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
已知f(x)=cosx•sin2x,下列命题错误的为( )
| A、y=f(x)为奇函数 | ||||
B、y=f(x)的图象关于x=
| ||||
C、y=f(x)的最大值为
| ||||
| D、y=f(x)为周期函数 |
把函数y=tanx(x∈{x|x≠
+kπ,k∈Z}的图象上所有点向左平行移动
个单位长度,再把所得图象上所有点的横坐标缩短到原来的
倍(纵坐标不变),得到的图象所表示的函数解析式是( )
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、y=tan(2x-
| ||||
B、y=tan(
| ||||
C、y=tan(2x+
| ||||
D、y=tan(2x+
|
如图,设全集U=N,集合A={1,3,5,7,8},B={1,2,3,4,5},则图中阴影部分表示的集合为( 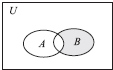

| A、{2,4} |
| B、{7,8} |
| C、{1,3,5} |
| D、{1,2,3,4,5} |
曲线y=xe2x-1在点(1,e)处切线的斜率等于( )
| A、2e | B、e | C、3e | D、1 |