题目内容
对于四面体ABCD,下列命题正确的是 (写出所有正确命题的编号)
①相对棱AB与CD所在的直线异面;
②若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
③分别作三组相对棱中点的连线,所得的三条线段相交于一点;
④最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
①相对棱AB与CD所在的直线异面;
②若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
③分别作三组相对棱中点的连线,所得的三条线段相交于一点;
④最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
考点:命题的真假判断与应用
专题:空间位置关系与距离,简易逻辑
分析:①假设相对棱AB与CD所在的直线共面,则A,B,C,D四点在同一平面内,与四面体ABCD矛盾,说明①正确;
②举特例说明②错误;
③由对应边中点的连线是平行四边形判断;
④不妨设AB为最长棱,分类讨论(i)当AC≥BD时,在△ACD中,由三角形的 两边之和大于第三边可得,AD+BD>AB,可判断(ii)当AC<BD时,在△ABC中,由三角形的 两边之和大于第三边可得AC+BC>AB,可判断.
②举特例说明②错误;
③由对应边中点的连线是平行四边形判断;
④不妨设AB为最长棱,分类讨论(i)当AC≥BD时,在△ACD中,由三角形的 两边之和大于第三边可得,AD+BD>AB,可判断(ii)当AC<BD时,在△ABC中,由三角形的 两边之和大于第三边可得AC+BC>AB,可判断.
解答:
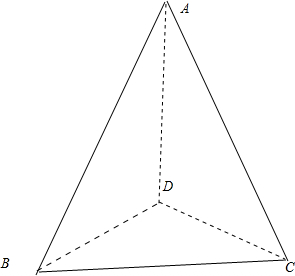 解:①假设相对棱AB与CD所在的直线共面,则A,B,C,D四点在同一平面内,与四面体ABCD矛盾,故①正确;
解:①假设相对棱AB与CD所在的直线共面,则A,B,C,D四点在同一平面内,与四面体ABCD矛盾,故①正确;
②当四面体的面ABC和ABD全等时,两条高所在的直线共面,命题②错误;
③对应边中点的连线是平行四边形对角线的交点,命题③正确;
④不妨设AB为最长棱,(i)当AC≥BD时,
在△ACD中,由三角形的 两边之和大于第三边可得,AD+BD>AB,则AD+AC≥AD+BD>AB;
(ii)当AC<BD时,在△ABC中,由三角形的 两边之和大于第三边可得AC+BC>AB,则DB+BC>BC+AC>AB.
故④正确.
故答案为:①③④.
 解:①假设相对棱AB与CD所在的直线共面,则A,B,C,D四点在同一平面内,与四面体ABCD矛盾,故①正确;
解:①假设相对棱AB与CD所在的直线共面,则A,B,C,D四点在同一平面内,与四面体ABCD矛盾,故①正确;②当四面体的面ABC和ABD全等时,两条高所在的直线共面,命题②错误;
③对应边中点的连线是平行四边形对角线的交点,命题③正确;
④不妨设AB为最长棱,(i)当AC≥BD时,
在△ACD中,由三角形的 两边之和大于第三边可得,AD+BD>AB,则AD+AC≥AD+BD>AB;
(ii)当AC<BD时,在△ABC中,由三角形的 两边之和大于第三边可得AC+BC>AB,则DB+BC>BC+AC>AB.
故④正确.
故答案为:①③④.
点评:本题考查异面直线,三垂线定理,棱锥的结构特征,考查空间想象能力逻辑思维能力,属于中档题.

练习册系列答案
相关题目
抛物线x2=py上一点M(x0,3)到焦点的距离为5,则实数p的值为( )
| A、-8 | B、4 | C、8 | D、16 |
记曲线y=sin
x,x∈[-3,1]与y=1所围成的封闭区域为D,若直线y=ax+2与D有公共点,则实数a的取值范围是( )
| π |
| 2 |
A、[-1,
| ||||
B、(-∞,-1]∪[
| ||||
C、[-
| ||||
D、(-∞,-
|