题目内容
19.某公司经营一批进价为每件4百元的商品,在市场调查时发现,此商品的销售单价x(百元)与日销售量y(件)之间有如下关系:| x(百元) | 5 | 6 | 7 | 8 | 9 |
| y(件) | 10 | 8 | 9 | 6 | 1 |
(2)借助回归直线方程请你预测,销售单价为多少百元(精确到个位数)时,日利润最大?
相关公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-b\overline x$.
分析 (1)求求出回归系数,即可y关于x的回归直线方程;
(2)销售价为x时的利润为(x-4)(-2x+20.8)=-2x2+28.8x-83.2,即可得出结论.
解答 解:(1)因为$\overline{x}$=7,$\overline{y}$=6.8,
所以,$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$=$\frac{218-5×7×6.8}{255-5×49}$=-2,$\widehata=\overline y-b\overline x$=20.8.
于是得到y关于x的回归直线方程y=-2x+20.8.
(2)销售价为x时的利润为(x-4)(-2x+20.8)=-2x2+28.8x-83.2,
当x=$\frac{28.8}{2×2}$≈7时,日利润最大.
点评 本题考查回归直线方程的求法和应用,考查最大利润的求法,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$与抛物线y2=2px(p>0)有公共焦点F且交于A,B两点,若直线AB过焦点F,则该双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
7.已知点A(x0,y0)是抛物线y2=2px(p>0)上一点,且它在第一象限内,焦点为F,O坐标原点,若|AF|=$\frac{3p}{2}$,|AO|=2$\sqrt{3}$,则此抛物线的准线方程为( )
| A. | x=-4 | B. | x=-3 | C. | x=-2 | D. | x=-1 |
14.已知命题p:直线$x+2y-\sqrt{2}=0$与直线$x+2y-6\sqrt{2}=0$之间的距离不大于1,命题q:椭圆2x2+27y2=54与双曲线9x2-16y2=144有相同的焦点,则下列命题为真命题的是( )
| A. | p∧(¬q) | B. | (¬p)∧q | C. | (¬p)∧(¬q) | D. | p∧q |
4.设a,b∈R,函数f(x)=ax+b(0≤x≤1),则f(x)>0恒成立是a+2b>0成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
8.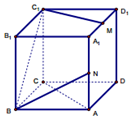 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④CD与BN为异面直线.
 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④CD与BN为异面直线.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.下列选项中,与sin2017°的值最接近的数为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{4}{5}$ |
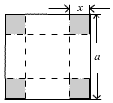 如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.
如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.