题目内容
9.已知等比数列{an}前n项和为Sn,且S3=8,S6=9,则公比q=$\frac{1}{2}$.分析 利用等比数列前n项和公式直接求解.
解答 解:∵等比数列{an}前n项和为Sn,且S3=8,S6=9,
∴依题意,$\frac{{S}_{6}}{{S}_{3}}$=$\frac{{a}_{1}(1-{q}^{6})}{{a}_{1}(1-{q}^{3})}$=1+q3=$\frac{9}{8}$,
解得q=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查等比数列的公比的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
1.已知椭圆的中心在原点,离心率e=$\frac{1}{2}$,且它的一个焦点与抛物线y2=-8x的焦点重合,则此椭圆方程为( )
| A. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{8}$+y2=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |
18.“$cosα=\frac{1}{2}$”是“$α=\frac{π}{3}$”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分也不必要条件 |
19.某公司经营一批进价为每件4百元的商品,在市场调查时发现,此商品的销售单价x(百元)与日销售量y(件)之间有如下关系:
(1)求y关于x的回归直线方程;
(2)借助回归直线方程请你预测,销售单价为多少百元(精确到个位数)时,日利润最大?
相关公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-b\overline x$.
| x(百元) | 5 | 6 | 7 | 8 | 9 |
| y(件) | 10 | 8 | 9 | 6 | 1 |
(2)借助回归直线方程请你预测,销售单价为多少百元(精确到个位数)时,日利润最大?
相关公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-b\overline x$.
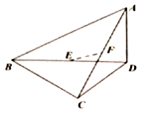 如图,三棱锥A-BCD中,BC⊥CD,AD⊥平面BCD,E、F分别为BD、AC的中点.
如图,三棱锥A-BCD中,BC⊥CD,AD⊥平面BCD,E、F分别为BD、AC的中点.