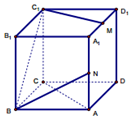如图.已知正方体ABCD-A1B1C1D1.M.N分别为A1D1和AA1的中点.则下列四种说法中正确的个数为( )①C1M∥AC,②BD1⊥AC,③BC1与AC的所成角为60°,④CD与BN为异面直线．A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

8．

如图，已知正方体ABCD-A₁B₁C₁D₁，M，N分别为A₁D₁和AA₁的中点，则下列四种说法中正确的个数为（　　）
①C₁M∥AC；
②BD₁⊥AC；
③BC₁与AC的所成角为60°；
④CD与BN为异面直线．

A．

B．

C．

D．

分析在①中，C₁M与AC是异面直线；在②中，由AC⊥平面BDD₁，知BD₁⊥AC；在③中，由AC∥A₁C₁，BC=A₁C₁=BA₁，知BC₁与AC的所成角为60°；在④中，由CD∥AB，AB∩BN=B，知CD与BN既为异面直线．

解答解：由正方体ABCD-A₁B₁C₁D₁，M，N分别为A₁D₁和AA₁的中点，知：
在①中，AC∥A₁C₁，A₁C₁∩C₁M=C₁，∴C₁M与AC是异面直线，故①错误；
在②中，∵AC⊥DD₁，AC⊥BD，BD∩DD₁=D，
∴AC⊥平面BDD₁，又BD?平面BDD₁，故BD₁⊥AC，故②正确；
在③中，AC∥A₁C₁，BC=A₁C₁=BA₁，∴BC₁与AC的所成角为60°，故③正确；
在④中，CD∥AB，AB∩BN=B，故CD与BN既为异面直线，故④正确．
故选：C．

点评本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置的关系的合理运用．

练习册系列答案

成长记寒假总动员云南科技出版社系列答案

	A．	充要条件		B．	充分不必要条件
	C．	必要不充分条件		D．	不充分也不必要条件

19．某公司经营一批进价为每件4百元的商品，在市场调查时发现，此商品的销售单价x（百元）与日销售量y（件）之间有如下关系：

x（百元）	5	6	7	8	9
y（件）	10	8	9	6	1

（1）求y关于x的回归直线方程；
（2）借助回归直线方程请你预测，销售单价为多少百元（精确到个位数）时，日利润最大？
相关公式：$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\widehata=\overline y-b\overline x$．

16．以下四个命题中，错误命题的序号是（　　）

	A．	△ABC中，若a＞b，则sinA＞sinB
	B．	函数y=f（x）在x=x₀处取得极值的充要条件是f'（x₀）=0
	C．	等差数列{a_n}中，a₄=4，a₅+a₁₁=16则a₁₂=12
	D．	双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离3．