题目内容
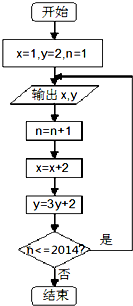根据如图所示的程序框图，将输出的x值依次记为x1，x2，x3，…，x2014；输出的y值依次记为y1，y2，y3，…，y2014（Ⅰ）求数列{xn}，{yn}的通项公式；
（Ⅱ）若数列{zn}满足
| z1 |
| y1 |
| z2 |
| y2 |
| z3 |
| y3 |
| zn |
| yn |
考点：程序框图
专题：等差数列与等比数列,算法和程序框图
分析：（I）利用等差数列的通项公式求出数列{xn}的通项公式，利用归纳法求得数列{yn}的通项公式；
（II）根据数列{zn}满足
+
+
+…+
=xn+1，分别求得Z1与n≥2时Zn，求出数列{zn}的通项公式，利用等比数列的前n项和公式求数列{zn}前n项之和Sn．
（II）根据数列{zn}满足
| z1 |
| y1 |
| z2 |
| y2 |
| z3 |
| y3 |
| zn |
| yn |
解答：
解：（Ⅰ）由程序框图可知：{xn}是等差数列，且首项x1=1，公差d=2，∴xn=1+2（n-1）=2n-1，
y1=2=3-1，y2=3×2+2=8=32-1，
y3=3×8+2=26=33-1，
y4=3×26+2=80=34-1，
∴yn=3n-1．
（Ⅱ）n=1时，z1=y1（x1+1）=4，
n≥2，
=2xn+1-2xn-1-1=2，∴Zn=2×yn=2×（3n-1），
∴Zn=2×（3n-1），n≥1．
∴Sn=2×
-2n=3n+1-2n-3
故∴Sn=3n+1-2n-3(1≤n≤2014)．
y1=2=3-1，y2=3×2+2=8=32-1，
y3=3×8+2=26=33-1，
y4=3×26+2=80=34-1，
∴yn=3n-1．
（Ⅱ）n=1时，z1=y1（x1+1）=4，
n≥2，
| Zn |
| yn |
∴Zn=2×（3n-1），n≥1．
∴Sn=2×
| 3(1-3n) |
| 1-3 |
故∴Sn=3n+1-2n-3(1≤n≤2014)．
点评：本题借助程序框图考查了求数列的通项公式及前n项和公式，熟练掌握等差数列的通项公式及等比数列的前n项公式是解答本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目